Шулуун (математик)

Шулуун шугам эсвэл товчоор шулуун гэдэг нь геометрийн элемент бөгөөд, төгсгөлгүй эгц үргэлжлэх, захын цэггүй, 0 өргөнтэй дүрс юм. Төгсгөлөг урт бүхий (2 захын цэг бүхий) шулууны хэсгийг хэрчим, нэг захын цэг бүхий шулууны хэсгийг цацраг гэдэг.
Тодорхойлолт: Шулуун нь төгсгөлгүй урт, төгсгөлгүй нарийн болоод хоёр чиглэлдээ хязгаарлагдахгүй шугамыг шулуун гэж нэрлэнэ. Эхлэлтэй төгсгөлгүй шугамыг цацраг гэнэ. Эхлэл төгсгөлтэй шугамыг хэрчим гэнэ. Харин цэгийг тодорхойлолтгүй авч үздэг билээ.
Ерөнхий ойлголт[засварлах | кодоор засварлах]
Евклидийн геометрт шулуун гэдэг нь тодорхойлолтгүй хэрэглэгддэг. Өөрөөр хэлбэл, "Шулуун гэж юу вэ?" гэсэн асуултад шууд хариулагдах тодорхойлолтыг ашигладаггүй, зөвхөн түүний шинж чанаруудыг дурьдсан теорем, аксиом, постулатуудыг ашиглан тодорхойлно.
- 2 ялгаатай цэгийг дайрсан шулуун цор ганц оршино.
- Нэг шулуун ба түүн дээр үл орших нэг цэг өгөгдвөл, өгөгдсөн цэгийг дайрсан, өгөгдсөн шулуунтай параллель шулуун цор ганцыг татаж болно.
Эдгээрээс "2 ялгаатай шулуун нь хамгийн ихдээ 1 цэгээр огтлолцоно" гэсэн шинж чанарыг хэлж чадна. Түүнчлэн 2 ялгаатай хавтгай нь хамгийн ихдээ 1 шулуунаар огтлолцдог.
Ерөнхий тохиолдолд шулуун ба хэрчим нь чиглэлгүй байдаг. Өөрөөр хэлбэл, A ба B цэгийг холбосон шулууныг AB гэж бичвэл, AB = BA болно. Эсрэгээр, хэрчимд чиглэл тогтоож болох бөгөөд тэр тохиолдолд AB ≠ BA гэж ойлгоно.
Евклидийн огторгуйд чиглэл бүхий хэрчмүүдийг, түүний эхлэлийн цэг ямар байхаас үл хамааран, чиглэл ба уртаар нь ангилсан ойлголтыг вектор гэдэг.
Евклидийн геометрт шулуун нь "эгц шулуун" үргэлжилсэн зүйл гэж тодорхойлолтгүйгээр ойлгодог ч яг үнэндээ тийм байх албагүй билээ. Муруй огторгуй дахь Евклидийн биш геометр дахь шулуун нь Евклидийн геометрт муруйж харагддаг.
Шулууны тэгшитгэл[засварлах | кодоор засварлах]
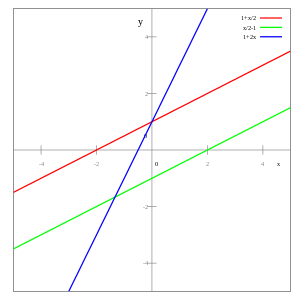
Тэгш өнцөгт координатын систем өгөгдсөн 2 хэмжээст Евклидийн огторгуй E2-гийн хувьд аливаа шулуун нь 1-зэргийн тэгшитгэлээр илэрхийлэгдэнэ.

