Вивианигийн теорем
Харагдац
Вивианигийн теорем нь Винченцо Вивианигийн нэрээр нэрлэгдсэн теорем бөгөөд "Адил талт гурвалжны доторх дурын цэгээс талууд хүртэлх зайнуудын нийлбэр нь уг гурвалжны өндөртэй тэнцүү" гэж томъёологдоно.
Уг теоремыг адил талт олон өнцөгт, адил өнцөгт олон өнцөгтүүдийн тухайд өргөтгөж болно. Тухайлбал, адил өнцөгт [эсвэл адил талт] олон өнцөгтийн дурын цэгээс талууд хүртэлх зайн нийлбэр нь тогтмол байдаг[1].
Баталгаа
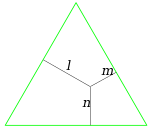
[засварлах | кодоор засварлах]Энэ теорем нь гурвалжнуудын талбайг харьцуулах замаар төвөггүй батлагдана. ABC нь адил талт гурвалжин, h нь түүний өндөр, s нь түүний талуудын урт байг. P нь гурвалжин доторх дурын цэг, ℓ, m, n нь P цэгээс талууд хүртэлх зайнууд гэе. Тэгвэл ABC гурвалжны талбай нь
болж бидний хүссэн зүйл батлагдлаа.
Эшлэл
[засварлах | кодоор засварлах]- Эрик Вейнштейн, Viviani's Theorem



