Компьютер дахь тооны илэрхийлэл

informatics

Өгөгдлийг компьютерт дүрслэх

Компьютер програмыг биелүүлэхийн тулд програм болон өгөгдлүүдийг шуурхай санах ойд түр зуур байрлуулна. Түүний хувьд програм ба өгөгдлийн хооронд ялгаа байхгүй бөгөөд бүгдийг нь өгөгдөл гэж “үзнэ”. Санах ой нь дараалсан олон жижиг хэсгүүдээс тогтсон байдаг. Нэг ийм хэсгийг нүд (cell) гэнэ. Нүд болгон өөрийн гэсэн үл давтагдах дугаартай байна. Түүнийг нь хаяг (address) гэнэ.

Нэг нүд ямар хэмжээний мэдээлэл хадгалах багтаамжтай вэ? Өнгөц бодоход 1 бит баймаар санагдавч тийм биш харин 8 бит байдаг байна. Тэгээд энэ 8 битийг 1 байт (byte) гэж нэрлэнэ. Учир нь ганц бит хангалттай мэдээллийг дүрсэлж чадахгүй. Харин бүлэг бит бол тэгж чадна. Жишээ нь 1 байт бол латин цагаан толгойн нэг үсгийг кодлоход яг хүрэлцдэг байна. Ийнхүү санах ойн нэгжээр битийг биш байтыг авсан учраас санах ойн нүд гэхийн оронд санах ойн байт, нүдийн хаяг гэхийн оронд байтын хаяг гэх мэтээр заримдаа ярьж, бичдэг. Харин байт дотроо битүүд нь 0-7 хүртэл дугаарлагдсан байна. Дугаар баруунаас зүүн тийш өсч эрэмбэлэгдэнэ.

1 байт хамгийн багадаа 00000000₂=0₁₀, хамгийн ихдээ 11111111₂=255₁₀=2⁸-1 гэсэн утга авна. Тиймээс нийтдээ 256₁₀=2⁸ янзын утга авах боломжтой. Түүнчлэн:

16-тын системд 1 байт гэдэг нь 2 нибл. Тэгэхээр 1 нибл бол хагас байт. Иймээс 16-тын 2 цифрээр нэг байтыг бичнэ. Тэгээд 2 байтыг 4 цифрээр, 4 байтыг 8 цифрээр г.м.

Компьютерын санах ойд өгөгдлийг хэрхэн дүрслэх вэ?

Эерэг бүхэл тоо

Санах ойд ихэвчлэн 1 юм уу 2 байт (нүд) эзэлдэг. Дүрслэхэд хамгийн хялбар. Шууд 2-тын бичлэгээр нь хадгалдаг. Тухайлбал, тооны 2-тын кодыг олж, шаардлагатай бол зүүн талд нь 0-үүд нэмээд, 1 байт (8 бит) эсвэл 2 байтын (16 бит) нүд эзлүүлнэ. 2 байтын тохиолдолд зүүн гар талын 8 битийг ахлах байт (high byte), баруун гар талын 8 битийг бага байт (low byte) гэх бөгөөд санах ойн дараалсан нүднүүдэд цуварч байрлана.

Зарим нэг жишээ.

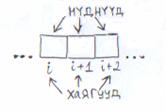
72₁₀ гэсэн тоог авч үзье.

Энд 72 гэсэн тоо санах ойн дурын i (болон i+1) хаягтай нүдэнд хэрхэн байрлахыг үзүүлжээ. Ганц байтын дүрслэлд бол хачирхалтай зүйл алга, тоо ганц нүдэнд байрлана. Харин 2 байтын дүрслэлээр, их хаягтай нүдэнд ахлах байт нь суусан байгааг анхаараарай. Энэ бол Pentium бүлийн процессоруудын онцлог юм.

1758₁₀ гэсэн тоог авч үзье. Үүнийг 1 байтаар дүрслэхэд багталцахгүйг анзаарсан байх аа (1758>255).

Хэрэв дүрслэх тоо 2 байтаас илүү зай эзлэх бол 4 байт зориулна. Гэхдээ ихэнх програмчлалын системд бүхэл тоон өгөгдлийн утгын мужийг дээд талаас нь 2³¹-оор (32-битийн процессор бүхий компьютерт) хязгаарладаг.

Дан эерэг утга авдаг бүхэл хэмжигдхүүн математик тооцоонд тийм ч их таардаггүй боловч компьютерын програм хангамжид өргөн хэрэглэгддэг. Ж.нь санах ойн нүдний хаяг дандаа эерэг бүхэл тоо байна. Мөн санах ойн нүдэнд хадгалагдах тоо өөрөө ямагт эерэг байх ёстой.

Тэмдэгт бүхэл тоо

Эерэг юм уу сөрөг утга авах боломжтой бүхэл тоог ингэж нэрийдсэнийг ойлгож буй байх. Санах ойд 1, 2 эсвэл 4 байт (нүд) эзэлдэг.

Хүн сөрөг тоог дүрслэхийн тулд “-” гэсэн тусгай тэмдгийг ашигладаг. Гэтэл компьютерын санах ойн нүд ямагт эерэг утга агуулж байхаар “цаанаасаа” зохицолдсон (1 байтын утгын муж 0..255). Тиймээс сөрөг тоог тэмдгийнх нь хамт шууд 2-тын бичлэгээр нь хадгалах боломжгүй юм. Ө.х. сөрөг тоог ямар нэг аргаар эерэг бүхэл тоо болгож кодлох хэрэгтэй болдог. Ингэхэд ямар аргууд хэрэглэгддэг вэ? Үүнд:

· Шууд код

· Нэмэлт код буюу Хоёрын гүйцээлт (Two’s complement)

г.м.

Эдгээр нь сөрөг тоог өөр өөрөөр кодлоно. Гэхдээ кодын хамгийн ахлах битийг тэмдгийн битээр сонгож авдгаараа адилхан. Энэ бит 1 байх нь “-”, 0 байх нь “+” тэмдгийг заана. Эерэг бүхэл тооны шууд ба нэмэлт код нь тэр тоо өөрөө байна.

· Шууд код

Хамгийн энгийн арга. Хамгийн ахлах битийг тэмдгийн битээр сонгож авна. Үлдсэн битүүдээр тооны абсолют утгыг дүрслэнэ. Ж.нь -1₁₀ гэсэн тоог 1 байтын форматаар шууд кодын аргаар дүрслэвэл:

Одоо -1₁₀+1₁₀=0₁₀ байгаа эсэхийг шалгаад үзье:

0-ийн оронд -2 гараад иржээ. Хэдийгээр кодлох процесс нь хялбар боловч ердийн нэмэх үйлдэл энэ аргад таарахгүй байна. Иймээс нэг бол сөрөг тоог нэмэх өөр арга зохиох эсвэл сөрөг тоог дүрслэх өөр арга олох хэрэгтэй болно.

· Нэмэлт код буюу 2-ын гүйцээлт

Энэ арга нь ямар нэг m гэсэн сөрөг тоог

2^N - |m| > 0

гэсэн ялгаврын 2-тын кодоор бичих явдал юм. Энд N - шаардлагатай битийн тоо (8, 16, 32 г.м.). |m| - модуль. Ө.х. сөрөг тооны модуль дээр нэмэхэд 2^N гарч байх тэр нэмэлтийг бичих учраас энэ аргыг Нэмэлт код гэдэг.

Гэхдээ практикт дээрх ялгаврыг шууд бодох нь тохиромжгүй байдаг. Учир нь 2^N-ыг олохын тулд нэмэлт бит шаардагдана. Ж.нь N=8 битийн форматаар (1 байтаар) бичнэ гэхэд 2⁸=256₁₀=1 0000 0000₂ гээд 9 бит буюу 0000 0001 0000 0000₂ гээд 2 байт болох нь ээ. Тиймээс Нэмэлт кодын оронд түүнтэй адил үр дүн өгдөг “2-ын гүйцээлт” хэмээх алгоритмыг ашиглана. Энэ алгоритмыг томъёолбол:

1. Сөрөг тооны модулийн 2-тын кодыг олох

2. Энэ кодын бит бүрийг инверслэх: 0-ийг 1, 1-ийг 0 болгох (үүнийг урвуу код гэнэ)

3. Гарсан код дээр 1-ийг нэмэх

алхмуудаас тогтоно. Эдгээрийг дэс дараалан гүйцэтгэхэд олдох кодыг m тооны 2-ын гүйцээлт гэдэг. Энэ нь бас m тооны нэмэлт код юм. Бас m тооны санах ой дахь дүрслэл болно. Ж.нь -5 гэсэн тооны 2-ын гүйцээлтийг 1 байтын форматаар олъё.

Одоо -5₁₀+5₁₀=0₁₀ байгаа эсэхийг шалгаад үзье:

Нийлбэр хэдийгээр 9 битийн урттай болсон ч 9 дэхь битийг компьютер “хаядаг”. Учир нь нийлбэрийн үр дүн 1 байтын урттай байх ёстой. Ингээд үлдсэн хэсэг 0 болж байна. Хариу зөв байна. Дээрх тооцоог 2, 4 байтын форматаар хийхэд адил чанараа алдахгүй.

Өөр нэгэн жишээ. -3₁₀–7₁₀=-10₁₀ болохыг үзэцгээе. Нэг байтын форматаар бичье.

Гарсан код дээр дахин “2-ын гүйцээлт” хийгээд -10 гэсэн тоо болохыг мэдэж болно.

Ийнхүү 2-ын гүйцээлтээр олсон кодуудыг ердийн нэмэх үйлдлээр нэмэх боломжтой байгаа нь түүний давуу тал юм. Орчин үеийн компьютерүүдэд энэ арга ихэвчлэн хэрэглэгддэг.

Хэрэв ямар нэг сөрөг тооны нэмэлт код өгөгдсөн үед түүнээс энэ тооны модулийг яаж олох вэ гэсэн асуулт мэдээж гарч ирнэ. Үүний тулд нэмэлт код дээр “2-ын гүйцээлт” хийнэ. Ингэхэд олдох код сөрөг тооны модуль байх болно. Ж.нь 11111000 гэсэн код өгөгджээ. Хэрэв энэ нь 2-ын гүйцээлт бол ямар сөрөг тоог дүрсэлсэн болохыг олъё:

-8₁₀ гэсэн тоог дүрсэлсэн байжээ.

Өгөгдлийн төрөл

Яг үнэндээ бол, санах ойн нүдэнд байрлах 2-тын код сөрөг тоог дүрсэлж байна уу, үгүй юу гэдгийг тухайн кодтой ажиллах машины команд шийддэг. Хэрэв командын алгоритмд “өгөгдлийг тэмдэгт бүхэл тоо гэж үз” гэсэн заавар байвал кодын ахлах битийг 1 байна уу, 0 байна уу гэдгийг шалгаад, 1 байвал түүнийг сөрөг тооны 2-ын гүйцээлт мэтээр “ойлгож” зохих үйлдлийг хийнэ. 0 байвал эерэг тоо гэж “ойлгоно”. Харин “эерэг тоо гэж үз” гэсэн заавар байвал кодыг шууд тэр чигээр нь “ойлгоно”. Өгөгдлийг ингэж өөр өөрөөр “хүлээн авдаг” командууд “Өгөгдлийн төрөл” (Data type) гэсэн ойлголттой салшгүй холбоотой. Энэ нь програмчлалын нэгэн чухал ойлголт (бүрдэл хэсэг) юм.

Бодит тоо

Бүхэл тоон олонлогоос ялгаатай нь бодит тоон олонлог бол тасралтгүй, мөн төгсгөлгүй байдаг. Тиймээс бүхэл тоонуудыг ямар нэг “но”-гүйгээр үл давтагдах төгсгөлөг 2-тын кодуудаар дүрсэлж болдог бол бодит тооны хувьд ийм биш. Ө.х. зарим бодит тоог төгсгөлөг кодоор дүрслэх боломжтой байхад зарим нь боломжгүй. Энэ талаар бид өмнө нь үзсэн.

Асуудлын гол нь компьютерын санах ой төгсгөлөг тооны нүдээс тогтдог явдал юм. Үүнээс шалтгаалан компьютерын ажиллаж чадах бодит тоон олонлог мөн дискрет, бас төгсгөлөг байх ёстой болно.

Компьютерын ухаанд бодит тоог хөвөгч цэгтэй тоо (floating-point number) гэж нэрлэдэг. Яагаад ингэдгийн учиртай танилцъя.

Дурын X бодит тоог p суурьт тооллын системд:

X = (±M) * p^±q

гэсэн зэрэгт хэлбэрээр бичиж болдог. Энд M-ийг X тооны мантисс (mantissa) гэж нэрлэнэ. Мантисс гэдэг нь тухайн тооны 0-ээс ялгаатай цифрүүдийг агуулсан үржигдэхүүн юм. Харин q-г X тооны p систем дэхь зэрэг (exponent) гэнэ. Ийм бичиглэлийг хөвөгч цэгтэй дүрслэл гэж нэрлээд байгаа. Ж.нь 30000.0 гэсэн тоог 3.0*10⁴, 0.3*10⁵, 0.03*10⁶ г.м.-ээр олон янз бичиж болно. Энд, бутархайн орны таслалыг “урагш, хойш хөдөлгөх” маягаар мантиссыг өөр өөр нарийвчлалтайгаар бичиж байна. Үүнийг зэргийн тусламжтайгаар гүйцэтгэнэ. Зэрэг нь мантиссын хамгийн эхний цифртэй харьцангуй таслалын байрлалыг зааж өгч байна. Ийм учраас хөвөгч цэгтэй тоо гэж нэрлэдэг. Дашрамд дурдахад бутархайн таслалын оронд цэгээр тэмдэглэдэг.

2-тын системийн хувьд энэ нь мөн хэрэгжинэ. Ж.нь 2,625₁₀ гэсэн тоог:

10.101₂ = 1.0101₂ * 2¹ = 0.10101₂ * 2¹⁰

г.м.-ээр бичнэ. Энд сүүлийн тооны зэргийг 2-тын кодоор бичсэнийг анхаараарай (10₂=2₁₀).

Компьютерын санах ойд бодит тоо яг ингэж мантисс ба зэрэг гэсэн хоёр хэсэг болон хадгалагддаг. Мантисс болон зэргийг дүрслэх битүүдийн тоог урьдаас тогтоосон байх болно.

Хэрэв хөвөгч цэг мантиссын хамгийн эхний 0-ээс ялгаатай цифрийн өмнө байрлаж байвал тухайн тоо хамгийн өндөр нарийвчлалтайгаар дүрслэгддэг байна. Үүний тулд мантиссыг ямагт 1-ээс бага, цэгийн яг ард талын цифр 0-ээс ялгаатай байхаар бичих хэрэгтэй. Ө.х.:

0.1₂ ≤ M < 1₂

нөхцлийг хангах ёстой. Энэ нөхцлийг хангаж дүрслэгдсэн тоог нормалчлагдсан (normalized) гэж нэрлэнэ. Ямар ч тоог хялбархан нормалчилж болно. Ж.нь

Сая дурдагдсан нормалчлал бол сонгодог хэлбэр юм. Нормалчлалын өөр хэлбэр бас бий. IBM PC төрлийн (Intel маркийн микропроцессор бүхий) компьютерүүдэд, хөвөгч цэг мантиссын хамгийн эхний 0-ээс ялгаатай цифрийн ард байрлаж байхаар дүрсэлдэг. Ө.х. мантиссын бүхэл хэсэг ямагт 1 байна: 1₂ ≤ M < 10₂

Ж.нь

Ийнхүү мантиссын эхний цифр ямагт 1 байх учраас тоог санах ойд хадгалахдаа энэ 1-ийг хаядаг. Мөн цэгийг ч дүрслэх шаардлагагүй. Ингэснээр бутархай хэсгийн дахиад нэг орныг нэмж хадгалах боломжтой болно. Ө.х. тоог дүрслэх нарийвчлалыг ихэсгэнэ. “Хаягдсан” 1-ийг “далд нэгж” (hidden bit) гэх бөгөөд яг тооцоо хийх болохоороо процессор мэдээж түүнийг “ил гаргаж ирдэг”.

Бодит тоо санах ойд 4 юм уу, 6, 8 эсвэл 10 байт (харгалзан 32, 48, 64, 80 бит) зай эзлэнэ. Ингэхдээ түүний бүх бүрдэл хэсгүүд:

• мантиссын тэмдэг

• мантисс

• зэргийн тэмдэг

• зэрэг

бүгд хадгалагдах ёстой. Гэхдээ мантиссыг хэдэн байтын урттай авах вэ, зэргийг хэдэн байтын урттай авах вэ, мантисс ба зэргийг ямар дарааллаар байрлуулах, тэдгээрийн тэмдгийг яаж тооцох вэ г.м. нь компьютерын төрлөөс хамаарч өөр өөр байж болно.

IBM PC төрлийн машинууд дараах загварыг (олон улсын IEEE Standard for Binary Floating-Point Arithmetic - ANSI/IEEE Std 754-1985 стандарт) баримталдаг. Энэ загварын дагуу, хэрэв тоо нийт n ширхэг битээр (n/8 байт) дүрслэгдэнэ гэвэл тэдгээрийн хамгийн ахлах байтын ахлах бит мантиссын тэмдгийг (0 – эерэг мантисс, 1 - сөрөг мантисс) үлдсэн n-1 ширхэг бит нь зүүнээс баруун тийш чиглэлд зэрэг ба мантиссыг хадгална.

Зэргийг санах ойд:

<Шилжсэн Зэрэг> = <Зэрэг> + 2^k-1-1

гэсэн томъёогоор хувиргаж хадгалдаг. Энд k бол зэргийг дүрслэх битийн тоо. Үүнийг зэргийн шилжүүлэлт гэнэ. Энэ нь зэрэг эерэг тоо юу сөрөг тоо гэдгээс үл хамааран түүнийг ямар нэг эерэг бүхэл тоогоор “орлуулж” байгаа хэрэг юм. Тоон дээр хийх арифметик үйлдлийн хурдыг ихэсгэж өгдөг ач холбогдолтой. Хэрэв зэрэг сөрөг тоо байвал түүний нэмэлт кодыг зэргийн оронд бичнэ гэдгийг сануулъя.

Мантиссыг дүрслэх битийн тоо түүний нарийвчлалыг тодорхойлдог нь ойлгомжтой. Битийн тоо олон байх тусам тооны нарийвчлал ихэснэ.

IEEE стандарт бодит тоог хадгалах дараах форматуудыг санал болгодог:

Жишээ авч үзье. -15.375₁₀ гэсэн тоог дан нарийвчлалаар хэрхэн кодлохыг харцгаая. 2-тын код нь -1111.011 байна. Нормалчилсны дараа -1.111011*2¹¹ болно. Бүхэл хэсгийг “хаявал”:

111011

болно. 11₂=3₁₀ гэсэн зэргийг шилжүүлбэл:

3 + 2^8-1 – 1 = 3 + 128 – 1 = 130₁₀ = 1000 0010₂

Одоо нийт 32 битийг зүүн гар талаас эхлэн бичнэ. 31 дугаартай хамгийн зүүн захын бит тэмдгийг заах учраас 1 байна (хасах тэмдэг):

1

30-р битээс эхлээд 23-р битийг дуусталх 8 битэд зэргийг бичнэ:

1 1000 0010

22-р битээс эхлээд 0-р битийг дуусталх 23 битэд мантиссыг бичнэ. Манай тохиолдолд мантисс маань 6 цифрээс тогтох тул үлдсэн 17 битийг шууд 0-ээр бөглөнө:

1 1000 0010 11101100000000000000000

Ингээд нийт 32 битийн урттай боллоо. Одоо үүнийг байт байтаар салгавал:

11000001 01110110 00000000 00000000

гэсэн 4 байт болно. Санах ойн дараалсан нүднүүдэд байрлахдаа хамгийн бага байт нь эхнийхэд, ахлах байт нь төгсгөлийнхэд очих тул:

00000000 00000000 01110110 11000001

Товчлохын үүднээс 16-тын кодоор бичвэл:

Өмнөх тоог давхар нарийвчлалаар дүрслэх байдал:

Компьютерын бодит тоон олонлог төгсгөлөг учраас дээд, доод хязгаар гэж мэдээж гарч ирнэ. Бодит тооны утгын мужийг түүний зэрэг нь тодорхойлдог. Дараах хүснэгтэд дан ба давхар нарийвчлалаар нормалчлагдан дүрслэгдэх тооны утгын мужийг харуулав. Хялбарыг бодож 10-тын тоогоор бичлээ.

Нормалчлагдсан тооны хувьд мантисс нь ямагт 0-ээс их байна гэдгийг дахин сануулъя.

Дан болон давхар нарийвчлалт дүрслэлийн хувьд дээрх хүснэгтэд ороогүй зарим онцгой тохиолдлууд бий. Эдгээрийг дараах хүснэгтэд харууллаа.

Бодит тооны арифметикт ±0 гэсэн хоёр 0 байдаг ажээ. Эдгээрийн мантисс нь адилхан 0, ганцхан тэмдгийн битээрээ ялгагдана. Нормалчлагдаагүй тоонууд бол хамгийн бага эерэг нормалчлагдсан тоо ба хамгийн их сөрөг нормалчлагдсан тооны хоорондох завсрыг (0-ийг оруулахгүйгээр) “бөглөнө”. 0-д маш ойрхон тоонууд гэсэн үг. Бодит тооны арифметикт ±∞ гэсэн хоёр ∞ байдаг ажээ. Хамгийн их эерэг нормалчлагдсан тооноос их бол +∞, хамгийн бага сөрөг нормалчлагдсан тооноос бага бол -∞ гэдэг байна. NaN гэсэн утга бол 0/0 г.м. байж болохгүй үйлдлийн үр дүнг илэрхийлнэ.

Ийнхүү бодит тоог компьютерт дүрслэх нь бүхэл тоог дүрслэхээс нэлээн төвөгтэй байна. Ийм тоотой ажиллахад зарцуулах хугацаа илүү болно. Нэгэнт л санах ой төгсгөлөг учраас тооны мантиссын дүрслэгдэх нарийвчлал бас анхнаасаа хязгаарлагдмал байна. Ө.х. дурын бодит тоог дүрсэлж чадахгүй. Тиймээс тэдгээр дээр хийсэн үйлдлийн үр дүн үргэлж тодорхой хэмжээний алдааг агуулж байх болно. Энэ алдааг үнэлнэ гэдэг бие даасан, нэлээн төвөгтэй ажил байдаг. Гэсэн хэдий ч орчин үеийн компьютер бодит тоотой төвөггүйхэн ажиллаж чаддаг. Ж.нь Intel маркийн микропроцессорууд (Pentium, Celeron г.м.) бүгд математик копроцессор (floating-point processor) хэмээх тусгай блокийг агуулах ба тэр нь бодит тоотой ажиллах бүх үйлдлийг гүйцэтгэж байдаг.