Хэрэглэгч:Timur/Ноорог/Газарзүйн координатын систем

Geodetic systems or geodetic data are used in geodesy, navigation, surveying by cartographers and satellite navigation systems to translate positions indicated on their products to their real position on earth.

The systems are needed because the earth is not a perfect sphere.

Examples of map data are:

• WGS 84, 72, 64 and 60 of the World Geodetic System
• NAD83, the North American Datum which is very similar to WGS84
• NAD27, the older North American Datum, of which NAD83 was basically a readjustment [1]
• OSGB36 of the Ordnance Survey of Great Britain
• ED50 : the European Datum

The difference in co-ordinates between data is commonly referred to as datum shift. The datum shift between two particular datums can vary from one place to another within one country or region, and can be anything from zero to hundreds of metres (or several kilometres for some remote islands). The North Pole, South Pole and Equator may be assumed to be in different positions on different datums, so True North may be very slightly different. Different datums use different estimates for the precise shape and size of the Earth (reference ellipsoids).

The difference between WGS84 and OSGB36 is up to 140 metres / 450 feet, which for some navigational purposes is an insignificant error. For most applications, such as surveying and dive site location for SCUBA divers, 140 metres is an unacceptably large error.

The main reason that there are a number of datums is that before the advent of GPS positioning, national map making organisations did not have a common surveying reference point and only produced maps for their locality.

Дэлхийн геометр ба түүн дээрх хэмжилт

Геоид ба үлгэр эллипсоид

The geoid is essentially the figure of the Earth abstracted from its topographic features. It is an idealized equilibrium surface of sea water, the mean sea level surface in the absence of currents, air pressure variations etc. and continued under the continental masses. The geoid, unlike the ellipsoid, is irregular and too complicated to serve as the computational surface on which to solve geometrical problems like point positioning. The geometrical separation between it and the reference ellipsoid is called the geoidal undulation. It varies globally between ±110 m.

A reference ellipsoid, customarily chosen to be the same size (volume) as the geoid, is described by its semi-major axis (equatorial radius) a and flattening f. The quantity f = (a−b)/a, where b is the semi-minor axis (polar radius), is a purely geometrical one. The mechanical ellipticity of the earth (dynamical flattening, symbol J₂) is determined to high precision by observation of satellite orbit perturbations. Its relationship with the geometric flattening is indirect. The relationship depends on the internal density distribution, or, in simplest terms, the degree of central concentration of mass.

The 1980 Geodetic Reference System (GRS80) posited a 6,378,137 m semi-major axis and a 1:298.257 flattening. This system was adopted at the XVII General Assembly of the International Union of Geodesy and Geophysics (IUGG). It is essentially the basis for geodetic positioning by the Global Positioning System and is thus also in extremely widespread use outside the geodetic community.

The numerous other systems which have been used by diverse countries for their maps and charts are gradually dropping out of use as more and more countries move to global, geocentric reference systems using the GRS80 reference ellipsoid.

Гурван хэмжээст координатын системүүд

The locations of points in three-dimensional space are most conveniently described by three cartesian or rectangular coordinates, $X,Y$ and $Z$. Since the advent of satellite positioning, such coordinate systems are typically geocentric: the $Z$ axis is aligned with the Earth's (conventional or instantaneous) rotation axis.

Before the satellite geodesy era, the coordinate systems associated with geodetic datums attempted to be geocentric, but their origins differed from the geocentre by hundreds of metres, due to regional deviations in the direction of the plumbline (vertical). These regional geodetic datums, such as ED50 (European Datum 1950) or NAD83 (North American Datum 1983) have ellipsoids associated with them that are regional 'best fits' to the geoids within their areas of validity, minimising the deflections of the vertical over these areas.

It is only because GPS satellites orbit about the geocentre, that this point becomes naturally the origin of a coordinate system defined by satellite geodetic means, as the satellite positions in space are themselves computed in such a system.

Geocentric coordinate systems used in geodesy can be divided naturally into two classes:

1. Inertial reference systems, where the coordinate axes retain their orientation relative to the fixed stars, or equivalently, to the rotation axes of ideal gyroscopes; the $X$ axis points to the vernal equinox
2. Co-rotating, also ECEF ("Earth Centred, Earth Fixed"), where the axes are attached to the solid body of the Earth. The $X$ axis lies within the Greenwich observatory's meridian plane.

The coordinate transformation between these two systems is described to good approximation by (apparent) sidereal time, which takes into account variations in the Earth's axial rotation (length-of-day variations). A more accurate description also takes polar motion into account, a phenomenon currently closely monitored by geodesists.

Хоёр хэмжээст координатын системүүд

In surveying and mapping, important fields of application of geodesy, two general types of coordinate systems are used in the plane:

1. Plano-polar, in which points in a plane are defined by a distance $s$ from a specified point along a ray having a specified direction $\alpha$ with respect to a base line or axis;
2. Rectangular, points are defined by distances from two perpendicular axes called $x$ and $y$. It is geodetic practice — contrary to the mathematical convention — to let the $x$ axis point to the North and the $y$ axis to the East.

Rectangular coordinates in the plane can be used intuitively with respect to one's current location, in which case the $x$ axis will point to the local North. More formally, such coordinates can be obtained from three-dimensional coordinates using the artifice of a map projection. It is not possible to map the curved surface of the Earth onto a flat map surface without deformation. The compromise most often chosen — called a conformal projection — preserves angles and length ratios, so that small circles are mapped as small circles and small squares as squares.

An example of such a projection is UTM (Universal Transverse Mercator). Within the map plane, we have rectangular coordinates $x$ and $y$. In this case the North direction used for reference is the map North, not the local North. The difference between the two is called meridian convergence.

It is easy enough to "translate" between polar and rectangular coordinates in the plane: let, as above, direction and distance be $\alpha$ and $s$ respectively, then we have

${\begin{matrix}x&=&s\cos \alpha \\y&=&s\sin \alpha \end{matrix}}$

The reverse translation is slightly more tricky.

Геодезийн өгөгдөл

Because geodetic point coordinates (and heights) are always obtained in a system that has been constructed itself using real observations, we have to introduce the concept of a geodetic datum: a physical realization of a coordinate system used for describing point locations. The realization is the result of choosing conventional coordinate values for one or more datum points.

In the case of height datums, it suffices to choose one datum point: the reference bench mark, typically a tide gauge at the shore. Thus we have vertical datums like the NAP (Normaal Amsterdams Peil), the North American Vertical Datum 1988 (NAVD88), the Kronstadt datum, the Trieste datum, etc.

In case of plane or spatial coordinates, we typically need several datum points. A regional, ellipsoidal datum like ED50 can be fixed by prescribing the undulation of the geoid and the deflection of the vertical in one datum point, in this case the Helmert Tower in Potsdam. However, an overdetermined ensemble of datum points can also be used.

Changing the coordinates of a point set referring to one datum, to make them refer to another datum, is called a datum transformation. In the case of vertical datums, this consists of simply adding a constant shift to all height values. In the case of plane or spatial coordinates, datum transformation takes the form of a similarity or Helmert transformation, consisting of a rotation and scaling operation in addition to a simple translation. In the plane, a Helmert transformation has four parameters, in space, seven.

In surveying and geodesy, a datum is a reference point or surface against which position measurements are made, and an associated model of the shape of the earth for computing positions. Horizontal datums are used for describing a point on the earth's surface, in latitude and longitude or another coordinate system. Vertical datums are used to measure elevations or underwater depths.

Хэвтээ өгөгдөл

The horizontal datum is the model used to measure positions on the earth. A specific point on the earth can have substantially different coordinates, depending on the datum used to make the measurement. There are hundreds of locally-developed horizontal datums around the world, usually referenced to some convenient local reference point. Contemporary datums, based on increasingly accurate measurements of the shape of the earth, are intended to cover larger areas. The WGS84 datum, which is almost identical to the NAD83 datum used in North America, is a common standard datum.

Босоо өгөгдөл

A vertical datum is used for measuring the elevations of points on the earth's surface. Vertical data are either tidal, based on sea levels, gravimetric, based on a geoid, or geodetic, based on the same ellipsoid models of the earth used for computing horizontal datums.

In common usage, elevations are often cited in height above sea level; this is a widely used tidal datum. Because ocean tides cause water levels to change constantly, the sea level is generally taken to be some average of the tide heights. Mean lower low water — the average of the lowest points the tide reached on each day during a measuring period of several years — is the datum used for measuring water depths on some nautical charts, for example; this is called the chart datum. Whilst the use of sea-level as a datum is useful for geologically recent topographic features, sea level has not stayed constant throughout geological time, so is less useful when measuring very long-term processes.

A geodetic vertical datum takes some specific zero point, and computes elevations based on the geodetic model being used, without further reference to sea levels. Usually, the starting reference point is a tide gauge, so at that point the geodetic and tidal datums might match, but due to sea level variations, the two scales may not match elsewhere. One example of a geoid datum is NAVD88, used in North America, which is referenced to a point in Quebec, Canada.

Нэр томъёоны талаар

In the abstract, a coordinate system as used in mathematics and geodesy is, e.g., in ISO terminology, referred to as a coordinate system. International geodetic organizations like the IERS (International Earth Rotation and Reference Systems Service) speak of a reference system.

When these coordinates are realized by choosing datum points and fixing a geodetic datum, ISO uses the terminology coordinate reference system, while IERS speaks of a reference frame. A datum transformation again is referred to by ISO as a coordinate transformation. (ISO 19111: Spatial referencing by coordinates).

Зарим чухал ойлголтууд

Here we define some basic observational concepts, like angles and coordinates, defined in geodesy (and astronomy as well), mostly from the viewpoint of the local observer.

• The plumbline or vertical is the direction of local gravity, or the line that results by following it. It is slightly curved.

• The zenith is the point on the celestial sphere where the direction of the gravity vector in a point, extended upwards, intersects it. More correct is to call it a <direction> rather than a point.

• The nadir is the opposite point (or rather, direction), where the direction of gravity extended downward intersects the (invisible) celestial sphere.

• The celestial horizon is a plane perpendicular to a point's gravity vector.

• Azimuth is the direction angle within the plane of the horizon, typically counted clockwise from the North (in geodesy and astronomy) or South (in France).

• Elevation is the angular height of an object above the horizon, Alternatively zenith distance, being equal to 90 degrees minus elevation.

• Local topocentric coordinates are azimuth (direction angle within the plane of the horizon) and elevation angle (or zenith angle) and distance.

• The North celestial pole is the extension of the Earth's (precessing and nutating) instantaneous spin axis extended Northward to intersect the celestial sphere. (Similarly for the South celestial pole.)

• The celestial equator is the intersection of the (instantaneous) Earth equatorial plane with the celestial sphere.

• A meridian plane is any plane perpendicular to the celestial equator and containing the celestial poles.

• The local meridian is the plane containing the direction to the zenith and the direction to the celestial pole.

Эллипсоид дээрх хэмжих нэгжүүд

Geographical latitude and longitude are stated in the units degree, minute of arc, and second of arc. They are angles, not metric measures, and describe the direction of the local normal to the reference ellipsoid of revolution. This is approximately the same as the direction of the plumbline, i.e., local gravity, which is also the normal to the geoid surface. For this reason, astronomical position determination, measuring the direction of the plumbline by astronomical means, works fairly well provided an ellipsoidal model of the figure of the Earth is used.

A geographic mile, defined as one minute of arc on the equator, equals 1,855.32571922 m. A nautical mile is one minute of astronomical latitude. The radius of curvature of the ellipsoid varies with latitude, being the longest at the pole and shortest at the equator as is the nautical mile.

A metre was originally defined as the 40 millionth part of the length of a meridian. This means that a kilometre is equal to (1/40,000) * 360 * 60 meridional minutes of arc, which equals 0.54 nautical miles. Similarly a nautical mile is on average 1/0.54 = 1.85185... km.

Хувьсал

In geodesy, temporal change can be studied by a variety of techniques. Points on the Earth's surface change their location due to a variety of mechanisms:

• Continental plate motion, plate tectonics
• Episodic motion of tectonic origin, esp. close to fault lines
• Periodic effects due to Earth tides
• Postglacial land uplift due to isostatic adjustment
• Various anthropogenic movements due to, e.g., petroleum or water extraction or reservoir construction.

The science of studying deformations and motions in the Earth's crust and the solid Earth as a whole is called geodynamics. Often, also study of the Earth's irregular rotation is included in its definition.

Techniques for studying geodynamic phenomena on the global scale include:

• satellite positioning by GPS and similar techniques,
• very long baseline interferometry (VLBI)
• satellite and lunar laser ranging.
• Regionally and locally, precise levelling,
• precise tacheometers
• monitoring gravity change,
• Synthetic Aperture Radar Interferometry (InSAR) using satellite images.

Геодезийн координатууд

In geodetic coordinates the Earth's surface is approximated by an ellipsoid and locations near the surface are described in terms of latitude ($\phi$), longitude ($\lambda$) and height ($h$). The ellipsoid is completely parameterised by the semi-major axis $a$ and the flattening $f$.

Map of Earth showing lines of latitude (horizontally) and longitude (vertically), Eckert VI projection; large version (pdf, 1.8MB)

A geographic coordinate system enables every location on the earth to be specified by the three coordinates of a spherical coordinate system aligned with the spin axis of the Earth.

Өргөрөг ба уртраг

Latitude phi (φ) and Longitude lambda (λ)

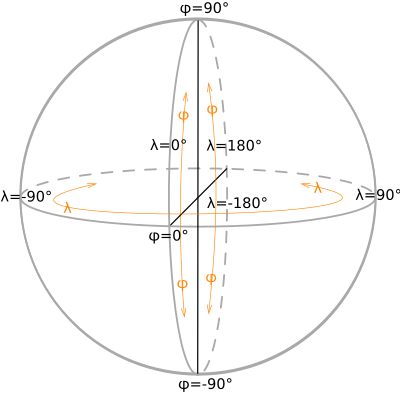
Borrowing from theories of the ancient Babylonians, later expanded by the famous Greek thinker and geographer Ptolemy, a full circle is divided into 360 degrees (360°).

• latitude (abbreviation: Lat.) is the angle at the centre of the co-ordinate system between any point on the earth's surface and the plane of the equator. Lines joining points of the same latitude are called parallels, and they trace concentric circles on the surface of the earth. Each pole is 90 degrees: the north pole 90° N; the south pole 90° S. The 0° parallel of latitude is designated the equator, an imaginary line that divides the globe into the Northern and Southern Hemispheres.
• longitude (abbreviation: Long.) is the angle east or west, at the centre of the co-ordinate system, between any point on the earth's surface and the plane of an arbitrary north-south line between the two geographical poles. Lines joining points of the same longitude are called meridians. All meridians are halves of great circles, and are not parallel: by definition they converge at the north and south poles. The line passing through the (former) Royal Observatory, Greenwich (near London in the UK) is the international zero-longitude reference line, the Prime Meridian. The antipodal meridian of Greenwich is both 180°W and 180°E.

By combining these two angles, the horizontal position of any location on Earth can be specified.

For example, Baltimore, Maryland (in the USA) has a latitude of 39.3° North, and a longitude of 76.6° West (Загвар:Coor d). So, a vector drawn from the center of the earth to a point 39.3° north of the equator and 76.6° west of Greenwich will pass through Baltimore.

This latitude/longitude "webbing" is known as the common graticule. There is also a complementary transverse graticule (meaning the graticule is shifted 90°, so that the poles are on the horizontal equator), upon which all spherical trigonometry is ultimately based.

Traditionally, degrees have been divided into minutes (1/60th of a degree, designated by ′ or "m") and seconds (1/60th of a minute, designated by ″ or "s"). There are several formats for degrees, all of them appearing in the same Lat-Long order:

• DMS Degree:Minute:Second (49°30'00"-123d30m00s)
• DM Degree:Minute (49°30.0'-123d30.0m)
• DD Decimal Degree (49.5000°-123.5000d), generally with 4 decimal numbers.

To convert from DM or DMS to DD, decimal degrees = whole number of degrees, plus minutes divided by 60, plus seconds divided by 3600. DMS is the most common format, and is standard on all charts and maps, as well as global positioning systems and geographic information systems.

The equator is the fundamental plane of all geographic coordinate systems. All spherical coordinate systems define such a fundamental plane.

Latitude and longitude values can be based on several different geodetic systems or datums, the most common being the WGS 84 used by all GPS equipment. In other words, the same point on the earth’s surface can be described by different latitude and longitude values depending on the reference datum.

In popular GIS software, data projected in latitude/longitude is often specified via a 'Geographic Coordinate System'. For example, data in latitude/longitude with the datum as the North American Datum of 1983 is denoted by 'GCS_North_American_1983'.

Өндөрлөг, өндөр, гүн

To completely specify a location on, in, or above the earth, one has to also specify the elevation, defined as the vertical position of the location relative to the centre of the reference system or some definition of the earth's surface. This is expressed in terms of the vertical distance to the earth below, but, because of the ambiguity of "surface" and "vertical", is more commonly expressed relative to a more precisely defined datum such as mean sea level (as height above mean sea level) or a geoid (a mathematical model of the shape of the earth's surface). The distance to the earth's center can be used both for very deep positions and for positions in space.

Other terms used with respect to the distance of a point from the earth's surface or some other datum are altitude, height, and depth.

Геодезийн ба дэлхий төвт өргөрөг

It is important to note that geodetic latitude ($\phi$) is different than geocentric latitude ($\phi '$). The geodetic latitude is determined by the normal to the ellipsoid whereas geocentric latitude is determined from the centre of the spheroid (see figure). Unless otherwise specified latitude is geodetic latitude.

Эллипсоидыг тодорхойлогч параметрүүд

Parameter	Symbol
Semi-major axis	a
Reciprocal of flattening	1/f

From a and f it is possible to derive the semi-minor axis b, first eccentricity e and second eccentricity e' of the ellipsoid

Parameter	Value
semi-minor axis	b = a(1-f)
First eccentricity squared	e2 = 1-b2/a2 = 2f-f2
Second eccentricity	e'2 = a2/b2 - 1 = f(2-f)/(1-f)2

Зарим өргөн хэрэглэгддэг системүүд

Currently the most common reference ellipsoid used, and that used in the context of the Global Positioning System, is WGS 84.

Traditional reference ellipsoids or geodetic datums are defined regionally and therefore non-geocentric, e.g., ED50. Modern geodetic datums are established with the aid of GPS and will therefore be geocentric, e.g., WGS 84.

The following table lists some of the most common ellipsoids:

Name	Equatorial axis (m)	Polar axis (m)	Inverse flattening, $1/f\,\!$
Clarke 1866	6 378 206.4	6 356 583.8	294.978 698 2
International 1924	6 378 388	6 356 911.9	297.0
GRS 1980	6 378 137	6 356 752.3141	298.257 222 101
WGS 1984	6 378 137	6 356 752.3142	298.257 223 563
Sphere (6371 km)	6 371 000	6 371 000	0

See Figure of the Earth for a more complete historical list.

A more comprehensive list of geodetic systems can be found here

• Australian Geodetic Datum 1966 [AGD66] and Australian Geodetic Datum 1984 (AGD84)

AGD66 and AGD84 both use the parameters defined by Australian National Spheroid (see below)

• Australian National Spheroid (ANS)

ANS Defining Parameters

Parameter	Notation	Value
semi-major axis	a	6378160.000m
Reciprocal of Flattening	1/f	298.25

• Geocentric Datum of Australia 1994 (GDA94) and Geocentric Datum of Australia 2000 (GDA2000)

Both GDA94 and GDA2000 use the parameters defined by GRS80 (see below)

• Geodetic Reference System 1980 (GRS80)

GRS80 Defining Parameters

Parameter	Notation	Value
semi-major axis	a	6378137m
Reciprocal of Flattening	1/f	298.257222101

see GDA Technical Manual document for more details.

• World Geodetic System 1984 (WGS84)

The global positioning system (GPS) uses the world geodetic system 1984 (WGS84) to determine the location of a point near the surface of the Earth.

WGS84 Defining Parameters

Parameter	Notation	Value
semi-major axis	a	6378137.0m
Reciprocal of Flattening	1/f	298.257223563

WGS84 derived geometric constants

Constant	Notation	Value
Semi-minor axis	b	6356752.3142m
First Eccentricity Squared	e2	6.69437999014x10-3
Second Eccentricity Squared	e'2	6.73949674228x10-3

see The official World Geodetic System 1984 document for more details.

Бусад координатын системүүд

Local tangent plane

Дэлхий төвт дэлхийд холбоотой (ДТДХ) координатууд

The Earth centred Earth fixed (ECEF) coordinate system rotates with the Earth and has its origin at the centre of the Earth. The $X$ axis passes through the equator at the prime meridian. The $Z$ axis passes through the north pole. The $Y$ axis can be determined by the right hand rule to be passing through the equator at 90^o longitude.

Локаль дорно умар дээш (ДУД) координатууд

In many targeting and tracking applications the local East, North, Up (ENU) Cartesian coordinate system is far more intuitive and practical than ECEF or Geodetic coordinates. By convention the east axis is labeled $x$, the north $y$ and the up $z$.

Локаль умар дорно доош (УДД) координатууд

In an aeroplane most objects of interest are below you, it is therefore sensible to define down as a positive number, the NED coordinates allow you to do this. By convention the north axis is labeled $x'$, the east $y'$ and the down $z'$. To avoid confusion between $x$ and $x'$, etc in this web page we will restrict the local coordinate frame to ENU.

Координатын хувиргалт

Геодезийн координатаас ДУД руу

To convert from geodetic coordinates to local ENU up coordinates is a two stage process

1. Convert geodetic coordinates to ECEF coordinates
2. Convert ECEF coordinates to local ENU coordinates

Геодезийн координатаас ДТДХ руу

Geodetic coordinates (latitude $\phi$, longitude $\lambda$, height $h$) can be converted into ECEF coordinates using the following formulae:

${\begin{matrix}X&=&\left({\frac {a}{\chi }}+h\right)\cos {\phi }\cos {\lambda }\\Y&=&\left({\frac {a}{\chi }}+h\right)\cos {\phi }\sin {\lambda }\\Z&=&\left({\frac {a(1-e^{2})}{\chi }}+h\right)\sin {\phi }\end{matrix}}$

Where $\chi ={\sqrt {1-e^{2}\sin ^{2}{\phi }}},$ $a$ and $e^{2}$ are the semi-major axis and the square of the first numerical eccentricity of the ellipsoid respectively

ДТДХ коорднатаас ДУД руу

Local tangent plane

To transform from ECEF coordinates to the local coordinates we need a local reference point, typically this might be the location of the radar. If a radar is located at $\{X_{r},Y_{r},Z_{r}\}$ and an aircraft at $\{X_{p},Y_{p},Z_{p}\}$ then the vector pointing from the radar to the aircraft in the ENU frame is

${\begin{bmatrix}x\\y\\z\\\end{bmatrix}}={\begin{bmatrix}-\sin \lambda &\cos \lambda &0\\-\sin \phi '\cos \lambda &-\sin \phi '\sin \lambda &\cos \phi '\\\cos \phi '\cos \lambda &\cos \phi '\sin \lambda &\sin \phi '\end{bmatrix}}{\begin{bmatrix}X_{p}-X_{r}\\Y_{p}-Y_{r}\\Z_{p}-Z_{r}\end{bmatrix}}$

Note: $\phi '$ is the geocentric latitude and is calculated by

$\tan \phi '={\frac {Z_{r}}{\sqrt {X_{r}^{2}+Y_{r}^{2}}}}$

The geocentric and geodetic longitude have the same value

$\tan \lambda ={\frac {Y_{r}}{X_{r}}}$

Note: Unambiguous determination of $\phi '$ and $\lambda$ requires knowledge of which quadrant the coordinates lie in.

ДУД-ээс геодезийн координат руу

As before it is done in two stages

1. Convert local ENU coordinates to ECEF coordinates
2. Convert ECEF coordinates to GPS coordinates

ДУД-ээс ДТДХ руу

This is just the inversion of the ECEF to ENU transformation so

${\begin{bmatrix}X\\Y\\Z\\\end{bmatrix}}={\begin{bmatrix}-\sin \lambda &-\sin \phi '\cos \lambda &\cos \phi '\cos \lambda \\\cos \lambda &-\sin \phi '\sin \lambda &\cos \phi '\sin \lambda \\0&\cos \phi '&\sin \phi '\end{bmatrix}}{\begin{bmatrix}x\\y\\z\end{bmatrix}}+{\begin{bmatrix}X_{r}\\Y_{r}\\Z_{r}\end{bmatrix}}$

ДТДХ-оос геодезийн координат руу

The conversion of ECEF coordinates to geodetic coordinates (such WGS84) is a much harder problem. A number of techniques are available but the most accurate according to Zhu (Ref 8), is the following 15 step procedure summarised by Kaplan. It is assumed that geodetic parameters $\{a,b,e,e'\}$ are known

${\begin{matrix}r&=&{\sqrt {X^{2}+Y^{2}}}\\E^{2}&=&a^{2}-b^{2}\\F&=&54b^{2}Z^{2}\\G&=&r^{2}+(1-e^{2})Z^{2}-e^{2}E^{2}\\C&=&{\frac {e^{4}Fr^{2}}{G^{3}}}\\S&=&{\sqrt[{3}]{1+C+{\sqrt {C^{2}+2C}}}}\\P&=&{\frac {F}{3\left(S+{\frac {1}{S}}+1\right)^{2}G^{2}}}\\Q&=&{\sqrt {1+2e^{4}P}}\\r_{0}&=&{\frac {-(Pe^{2}r)}{1+Q}}+{\sqrt {{\frac {1}{2}}a^{2}\left(1+1/Q\right)-{\frac {P(1-e^{2})Z^{2}}{Q(1+Q)}}-{\frac {1}{2}}Pr^{2}}}\\U&=&{\sqrt {(r-e^{2}r_{0})^{2}+Z^{2}}}\\V&=&{\sqrt {(r-e^{2}r_{0})^{2}+(1-e^{2})Z^{2}}}\\Z_{0}&=&{\frac {b^{2}Z}{aV}}\\h&=&U\left(1-{\frac {b^{2}}{aV}}\right)\\\phi &=&\arctan \left[{\frac {Z+e'^{2}Z_{0}}{r}}\right]\\\lambda &=&\arctan[{\frac {Y}{X}}]\end{matrix}}$

Note: Unambiguous determination of $\lambda$ requires knowledge of the quadrant

Мөн үзэх

• Automotive navigation system
• Geographic information system (GIS)
• Geographic coordinate conversion
• Geocodes
• Geo (microformat) - for marking-up coordinates in (X)HTML
• Global Positioning System (GPS).
• Great-circle distance the shortest distance between any two points on the surface of a sphere, and explains how to find that quantity if one knows the two latitudes and longitudes.
• Map projection
• Tropic of Cancer
• Tropic of Capricorn
• Universal Transverse Mercator coordinate system

Ном хэвлэл

1. List of geodetic parameters for many systems
2. Kaplan, Understanding GPS: principles and applications, 1 ed. Norwood, MA 02062, USA: Artech House, Inc, 1996.
3. GPS Notes
4. Introduction to GPS Applications
5. P. Misra and P. Enge, Global Positioning System Signals, Measurements, and Performance. Lincoln, Massachusetts: Ganga-Jamuna Press, 2001.
6. J. Zhu, "Conversion of Earth-centered Earth-fixed coordinates to geodetic coordinates," Aerospace and Electronic Systems, IEEE Transactions on, vol. 30, pp. 957-961, 1994.
7. P. Misra and P. Enge, Global Positioning System Signals, Measurements, and Performance. Lincoln, Massachusetts: Ganga-Jamuna Press, 2001.
8. Peter H. Dana: Geodetic Datum Overview - Large amount of technical information and discussion.
9. UK Ordnance Survey
10. US National Geodetic Survey

Гадны линкүүд

• Mathematics Topics-Coordinate Systems
• Geographic coordinates of countries (CIA World Factbook)
• Worldwide Geogr.Coordinates & Satellite images
• Global Gazetteer
• Coordinate converter