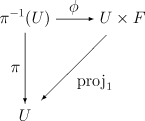Хэрэглэгч:Timur/Ноорог/Ширхэг багц

A cylindrical hairbrush showing the intuition behind the word "fiber bundle". This hairbrush is like a fiber bundle in which the base space is a cylinder and the fibers (bristles) are line segments. The mapping π:E→B would take a point on any bristle and map it to the point on the cylinder where bristle attaches.

In mathematics, in particular in topology, a fiber bundle (or fibre bundle) is a space which looks locally like a product space. It may have a different global topological structure in that the space as a whole may not be homeomorphic to a product space. Every fiber bundle consists of a continuous surjective map

\pi :E\to B

where small regions in the total space E look like small regions in the product space B × F. Here B is the base space while F is the fiber space. For example, setting E as the product space B × F, equipped with π = pr₁ (projection onto the first coordinate), is a fiber bundle. This is called the trivial bundle. One goal of the theory of bundles is to quantify, via algebraic invariants, what it means for a bundle to be non-trivial, or in other words twisted in the large.

Fiber bundles generalize vector bundles, where the main example is the tangent bundle of a manifold, as well as principal bundles. They play an important role in the fields of differential topology and differential geometry. They are also a fundamental concept in the mathematical formulation of gauge theory. Fiber bundles specialize the more general bundle.

Формаль тодорхойлолт

A fiber bundle consists of the data (E, B, π, F), where E, B, and F are topological spaces and π : E → B is a continuous surjection satisfying a local triviality condition outlined below. B is called the base space of the bundle, E the total space, and F the fiber. The map π is called the projection map. We shall assume in what follows that the base space B is connected.

We require that for any x in B, there is an open neighborhood U of x (which will be called a trivializing neighborhood) such that π⁻¹(U) is homeomorphic to the product space U × F, in such a way that π carries over to the projection onto the first factor. That is, the following diagram should commute:

where proj₁ : U × F → U is the natural projection and φ : π⁻¹(U) → U × F is a homeomorphism. The set of all {(U_i, φ_i)} is called a local trivialization of the bundle.

For any x in B, the preimage π⁻¹(x) is homeomorphic to F and is called the fiber over x. A fiber bundle (E, B, π, F) is often denoted

F\longrightarrow E\ {\xrightarrow {\,\ \pi \ }}\ B

to indicate a short exact sequence of spaces. Note that every fiber bundle π : E → B is an open map, since projections of products are open maps. Therefore B carries the quotient topology determined by the map π.

A smooth fiber bundle is a fiber bundle in the category of smooth manifolds. That is, E, B, and F are required to be smooth manifolds and all the functions above are required to be smooth maps. This is the most common context in which fiber bundles are studied and used.

Жишээнүүд

Тривиал багц

Let E = B × F and let π : E → B be the projection onto the first factor. Then E is a fiber bundle (of F) over B. Here E is not just locally a product but globally one. Any such fiber bundle is called a trivial bundle.

Мобиусийн цагираг

The Möbius strip is a nontrivial bundle over the circle.

Perhaps the simplest example of a nontrivial bundle E is the Möbius strip. The Möbius strip has a circle for a base B and a line segment for the fiber F, so the Möbius strip is a bundle of the line segment over the circle. A neighborhood U of a point x ∈ B is an arc; in the picture, this is the length of one of the squares. The preimage $\pi ^{-1}(U)$ in the picture is a (somewhat twisted) slice of the strip four squares wide and one long. The homeomorphism φ maps the preimage of U to a slice of a cylinder: curved, but not twisted.

The corresponding trivial bundle B × F would be a cylinder, but the Möbius strip has an overall "twist". Note that this twist is visible only globally; locally the Möbius strip and the cylinder are identical (making a single vertical cut in either gives the same space).

Клейний лонх

A similar nontrivial bundle is the Klein bottle which can be viewed as a "twisted" circle bundle over another circle. The corresponding trivial bundle would be a torus, S¹ × S¹.

The Klein bottle immersed in three-dimensional space.

Хучих буулгалт

A covering space is a fiber bundle such that the bundle projection is a local homeomorphism. It follows in particular, that the fiber is a discrete space.

Вектор ба гол багцууд

A special class of fiber bundles, called vector bundles, are those whose fibers are vector spaces (to qualify as a vector bundle the structure group of the bundle — see below — must be a linear group). Important examples of vector bundles include the tangent bundle and cotangent bundle of a smooth manifold. From any vector bundle, one can construct the frame bundle of bases which is a principal bundle (see below).

Another special class of fiber bundles, called principal bundles, are bundles on whose fibers a free and transitive group action by G is given, so that each fiber is a principal homogeneous space. The bundle is often specified along with the group by referring to it as a principal G-bundle. The group G is also the structure group of the bundle. Given a representation ρ of G on a vector space V, a vector bundle with ρ(G)⊆Aut(V) as a structure group may be constructed, known as the associated bundle.

Бөмбөлөг багц

A sphere bundle is a fiber bundle whose fiber is an n-sphere. Given a vector bundle E with a metric (such as the tangent bundle to a Riemannian manifold) one can construct the associated unit sphere bundle, for which the fiber over a point x is the set of all unit vectors in E_x. When the vector bundle in question is the tangent bundle T(M), the unit sphere bundle is known as the unit tangent bundle, and is denoted UT(M).

A sphere bundle is partially characterized by its Euler class, which is a degree n+1 cohomology class in the total space of the bundle. In the case n=1 the sphere bundle is called a circle bundle and the Euler class is equal to the first Chern class, which characterizes the topology of the bundle completely. For any n, given the Euler class of a bundle, one can calculate its cohomology using a long exact sequence called the Gysin sequence.

Огтлолууд

A section (or cross section) of a fiber bundle is a continuous map f : B → E such that π(f(x))=x for all x in B. Since bundles do not in general have globally-defined sections, one of the purposes of the theory is to account for their existence. This leads to the theory of characteristic classes in algebraic topology.

Often one would like to define sections only locally (especially when global sections do not exist). A local section of a fiber bundle is a continuous map f : U → E where U is an open set in B and π(f(x))=x for all x in U. If (U, φ) is a local trivialization chart then local sections always exist over U. Such sections are in 1-1 correspondence with continuous maps U → F. Sections form a sheaf.

Бүтцийн бүлэг ба шижилтийн функцүүд

Fiber bundles often come with a group of symmetries which describe the matching conditions between overlapping local trivialization charts. Specifically, let G be a topological group which acts continuously on the fiber space F on the left. We lose nothing if we require G to act effectively on F so that it may be thought of as a group of homeomorphisms of F. A G-atlas for the bundle (E, B, π, F) is a local trivialization such that for any two overlapping charts (U_i, φ_i) and (U_j, φ_j) the function

\phi _{i}\phi _{j}^{-1}:(U_{i}\cap U_{j})\times F\to (U_{i}\cap U_{j})\times F

is given by

\phi _{i}\phi _{j}^{-1}(x,\xi )=(x,t_{ij}(x)\xi )

where t_ij : U_i ∩ U_j → G is a continuous map called a transition function. Two G-atlases are equivalent if their union is also a G-atlas. A G-bundle is a fiber bundle with an equivalence class of G-atlases. The group G is called the structure group of the bundle.

In the smooth category, a G-bundle is a smooth fiber bundle where G is a Lie group and the corresponding action on F is smooth and the transition functions are all smooth maps.

The transition functions t_ij satisfy the following conditions

$t_{ii}(x)=1$
$t_{ij}(x)=t_{ji}(x)^{-1}$
$t_{ik}(x)=t_{ij}(x)t_{jk}(x)$

The third condition applies on triple overlaps U_i ∩ U_j ∩ U_k and is called the cocycle condition (see Čech cohomology).

A principal G-bundle is G-bundle where the fiber F is a principal homogeneous space for the left action of G itself (equivalently, one can specify that the action of G on the fibre F is free and transitive). In this case, it is often a matter of convenience to identify F with G and so obtain a (right) action of G on the principal bundle.

Багц буулгалтууд

It is useful to have notions of mapping between bundles on B for the same type of fiber F. These are called bundle maps. The most common are the mappings between vector bundles that are linear on each fiber; these occur also for different bases, for example from one tangent bundle to another. Another kind is the bundle map of principal bundles, which is G-equivariant fiber by fiber. Загвар:Stub-section

Мөн үзэх

Ном хэвлэл

Norman Steenrod, The Topology of Fibre Bundles, Princeton University Press (1951). ISBN 0-691-00548-6.
David Bleecker, Gauge Theory and Variational Principles, Addison-Wesley publishing, Reading, Mass (1981). ISBN 0-201-10096-7.

Гадны линкүүд

Fiber Bundle, PlanetMath
Making John Robinson's Symbolic Sculpture `Eternity'