Зунгааралт

Өөр өөр зунгааралт бүхий шингэний хөдөлгөөн. Дээд шингэн нь доод шингэнээс илүү бага зунгааралттай байгаа учир тайван байдалд удаан орно. Зунгааралт нь физик хэмжигдэхүүн юм

Зунгааралт гэдэг нь шингэний өөр өөр хурдтай эгэл хэсгүүдийн мөргөлдөөний улмаас үүсэх физик шинж чанар юм. Хэрэв хоолой дундуур шингэн шахагдаж байна гэж үзвэл хоолойн тэнхлэг орчимд шингэн хурдтай хөдлөх ба эсрэгээр хоолойн ханаруу дөхөх тусам шингэний хөдөлгөөний хурд багасаж улмаар тэг болно. Үүний шалтгаан нь уг зунгааралтаас үүссэн хүчдэл бөгөөд, (мөн хоолойн эхлэл болон төгсгөлийн хоорондох даралт нөлөөлнө), шингэний эгэл хэсгүүд хоорондын болон хоолойн ханатай үрэлцэх хүчийг даван туулж хөдөлгөөний хадгалахыг эрмэлзэнэ.

Шингэн нь ямар нэгэн эсэргүүцлийн хүчгүй, шүргэх хүчдэл үүсдэггүй бол тэдгээрийг идеаль шингэн эсвэл төгс шингэн гэж нэрлэнэ. Тэг зунгааралт нь зөвхөн супер шингэнд маш бага температуртай үед ажиглагдана. Өөрөөр хэлбэл бусад бүх шингэн нь эерэг зунгааралттай байх ба техникийн хэлээр тэдгээрийг бодит буюу зунгааралттай шингэн гэнэ. Ердийн ярианд шингэн нь усны үзүүлэх зунгааралтаас их бол өтгөн, усны зунгааралтаас бага буюу норгох чадвар нь бага бол хэт шингэн гэж үздэг. Зунгааралт хэт ихтэй шингэний жишээ бол зөгийн бал, цаашилбал давирхай, зарим төрлийн резин гэх мэтийг дурьдаж болох юм.

Үгийн гарал үүсэл

Зунгааралт (англи: viscosity) нь "viscum" гэдэг Латин үгнээс гаралтай бөгөөд энэ нь цагаан борц буюу "mistletoe" ургамалын нэр ба шувууг барьж авахад зориулсан уг ургамлаас гаргаж авсан цавууг ийнхүү нэрлэдэг байсан байна. Монгол хэлэнд наалдамхай зүйлийг зунгаг гэдэг үгээр илэрхийлэх ба үүнээс үүсгэн зунгааралт хэмжээх физик хэмжигдэхүүнийг нэрлэжээ.

Тодорхойлолт

Динамик (шүргэх) зунгааралт

Хоёр хавтгайн хоорондох ламинар урсгал. Хавтгайн хөдөлгөөн болон шингэний үе хоорондын ялгаатай хөдөлгөөн нь шүргэлтийг бий болгоно. Энэ үед бий болох хүчийг шингэний зунгааралтын тусламжтай тодорхойлж болно.

Ерөнхий параллель чиглэлтэй урсгалд (энэ тохиолдол шулуун хоолойд ажиглагдана) шүргэх хүчдэл нь хурдны градиенттэй тэнцүү байна.

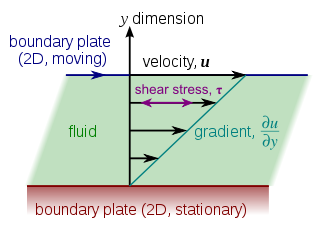
Шингэний динамик (шүргэх) зунгааралт нь өөр өөр хурдтай хөдөлж буй шингэний үе давхрагын хооронд бий болох шүргэлцэх эсэргүүцлийг илэрхийлнэ. Үүнийг Чоеттегийн урсгал гэж алдаршсан жишиг бодлогон дээр тодорхойлж болох ба энэ урсгал нь хоёр хавтгайн дунд шингэн орших ба дээд хавтай $u$ хурдтайгаар хөдөлж эхлэхэп ажиглагдана. (Хоёр хавтгайг ихэвчлэн хязгаагүй гэж авч үзэх ба тухайн урсгалын орчимд ирмэг болоод саад үл тулгарна.)

Хэрэв дээд хавтгайн хурд хангалттай бага бол, шингэний эгэл хэсэг хавтгайтай параллель хөдлөх ба хурдны хуваарилалт бараг шугаман байдлаар хувьсаж ёроолын хурд тэг, дээд хавтгайн хурд $u$ байна. Шингэнийг хавтгайтай параллель нимгэн үе давхргагаас бүрдэнэ гэж үзвэл дээрх байдлаар үе бүр өөрийн доод үеэсээ хурдан хөдлөх ба тэдгээр үеийн хоорондын үрэлт нь харьцангуй хөдөлгөөний улмаар бий болох хүчийг нэмэгдүүлнэ. Тухайлбал, шингэн дээд хавтгайд хөдөлгөөний эсрэг хүчээр үйлчилэх ба үүнтэй адилаар доод хавтгайд мөн хүч үйлчилнэ. Харин гадаад хүч нь дээд хавтгайн тогтмол хурдтай хөдөлгөөнийг хадгалахад чиглэнэ.

Хүч $F$ -ийн утга нь харьцангуй хурд $u$ , хавтгай бүрийн хөндлөн огтлолын талбай $A$ зэрэгт пропорциональ ба хавтгайн хоорондох зай $y$ -тай урвуу хамааралтай байна:

$F=\mu A{\frac {u}{y}}.$

Пропорционалийн коэффициент μ нь шингэний (өөрөөр хэлбэл динамик зунгааралт) зунгааралт юм.

Харьцаа $u/y$ нь хэв гажилтын утга эсвэл шүргэх хурд гэж нэрлэгдэх ба хавтгайгай перпендукляр шингэний хурдны уламжлал бөгөөд дифференциал хэлбэрийг хурдны градиент гэнэ. Исаак Ньютон зунгааралтын хүчний дифференциал хэлбэрийг дараах байдлаар өгчээ.

$\tau =\mu {\frac {\partial u}{\partial y}},$

Үүнд: $\tau =F/A$ ба ${\partial u}/{\partial y}$ нь хурдны градиент буюу орчны шүргэх хурдыг илэрхийлнэ. Энэ томъёонд урсгал нь босоо тэнхлэгтэй параллель байна. Энэ тэгшитгэл мөн хувьсах хурдтай үед хэрэглэгдэж болно. Өөрөөр хэлбэл хурд шугаман бус хуваарилалтай үед хүчинтэй.

Динамик зунгааралтын коэффициентийг ихэвчлэн Грек үсэг мю (μ) ашиглан тэмдэглэх ба инженер, химич, физикчдийн ихэнх нь үүнийг хэрэглэдэг. Гэхдээ, Онолын ба хэрэглээний химийн олон улсын холбооны гишүүнчлэлд Грек үсэг эта (η) хэрэглэхийг зөвлөдөг байна.

Кинематик зунгааралт

Кинематик зунгааралт (мөн "моментийн тархалтын коэф" гэж нэрлэх) нь динамик зунгааралт μ -г шингэний нягтад ρ харьцуулсанаар илэрхийлэгдэх ба ихэвчлэн Грек үсэг ню (ν)-гээр тэмдэглэгдэнэ.

$\nu ={\frac {\mu }{\rho }}$

Энэ нь Рейнольдсийн тоог шинжлэхэд тохиромжтой ухагдахуун болох ба Рейнольдсын тоо нь инерцийн хүч ба зунгааралтын хүчний харьцаагаар тдорхойлогдоно.

$Re={\frac {\rho uL}{\mu }}={\frac {uL}{\nu }}\;,$

Үүндe $L$ нь ердийн уртын хэмжигдэхүүн байна.

Эзлэхүүний зунгааралт

Шахагдах шингэн нь шүргэх хүчдэлгүйгээр шахагдах эсвэл тэлэлтийн үед урсгалыг эсэргүүцэж буй дотоод үрэлтийн хэлбэрийг харуулна. Эдгээр хэлбэр бүхий хүчнүүд нь тэлэлт ба шахагдах утгатай σ гэж тэмдэглэгдэх эзлэхүүний зунгааралт эсвэл бөөмийн зунгааралт (bulk) заримдаа хоёрдогч зунгааралт гэж нэрлэгдэх хүчин зүйлээр холбогддог.

Хэрэв шингэн нь дуу ба цохилтын долгион гэх мэт шиг sагшин зуур тэлж эсвэл агших тохиолдолд бөөмийн зунгааралт нь маш чухал параметр болно. Бөөмийн зунгааралт нь Дууны сулралын Стокесийн хууль ёсоор эдгээр долгион дахь энергийн алдагдлыг тайлбарладаг.

Зунгааралтын тенсор

Ерөнхийдөө шингэн дахь хүчдэлүүд нь хугацааны турш дахь (зунгааралтын хүчдэл) деформацийн өөрчлөлтийн утга, тайван төлөвөөс зарим хэсгийн деформац (уян харимхайн хүчдэл) зэргээр илэрхийлэгдэнэ. Шингэний механикт тодорхойлолтоороо уян харимхайн хүчдэл нь зөвхөн гидростатикийн даралтыг агуулна.

Маш ерөнхий илэрхийлэлд шингэний зунгааралт нь шингэний гажилтын утга ба зунгааралтын хүчдэлийн хоорондын хамаарлаар илэрхийлэгдэнэ гэж үздэг. Шугаман зураглалын тодорхойлолтоор илэрхийлэгдэх Ньютоны шингэний загварт энэ хамаарал нь зунгааралтын тенсороор дүрслэгдэх ба үүнийг гажих утгын тенсороор (хурдны градиент) үржвэл зунгааралтын хүчдэлийн тенсорыг өгнө.

Зунгааралтын тенсор нь үл хамаарах 9 чөлөөний зэрэгтэй байна. Изотропи Ньютоны шингэний хувьд эдгээр нь хоёр үл хамаарах параметрээр буурах боломжтой. Ихэнхдээ тенсорын задаргаа нь хүчдэлийн зунгааралт μ болон бөөмийн зунгааралт σ болно.

Нюьтоны ба Нюьтоны бус шингэнүүд

Материал бүрийн шугамын налуу, зунгааралт нь өөр өөр байна.

Зунгааралтын тухай Ньютоны хууль нь тогтоосон тэгшитгэл юм (Гукийн хууль, Фикийн хууль, Омын хууль гэх мэттэй адил). Өөрөөр хэлбэл энэ нь байгалийн хууль биш боловч маш ойролцоолсон байдлаар материалын шинж чанарыг илэрхийлж чадна.

Ньютоны хуулийн дагуу ажиллаж байгаа μ гэсэн зунгааралттай байгаа шингэн нь шүргэх хүчдэлээс хамааралтай байх бөгөөд Ньютоны шингэн гэж нэрлэгдэнэ. Хий, ус болон олон бусад ердийн шингэнүүдийг ердийн нөхцөлд Ньютоны шингэн гэж авч үзэж болох юм. Эдгээр шингэнтэй адил Ньютоны хуулиас ямар нэгэн байдлаар зөрдөг Ньютоны бус шингэнүүд байна. Тухайлбал:

• Өтгөрөх шингэн, Сунах хүчдэл ихсэхэд зунгааралт нэмэгддэг.
• Шингэрэх шингэн, Сунах хүчдэл ихэсхэд зунгааралт буурна.
• Тихотропи шингэнүүд, шахах, зайлах, хутгах, сэгсрэх үед улам шингэрэх шингэн.
• Реопектик шингэн, шахах, зайлах, хутгах, сэгсрэх үед улам өтгөрөх шингэн.
• Бингамын пластик шингэн, бага даралтанд хатуу материал шиг, гэвч даралт өгөхөд урсамтгай чанартай болно.

Шингэрэх шингэнүүд нт маш элбэг байх ба тэдгээрийг тихотропи шингэнээс ялгаатай авч үзэх хэрэгтэй.

Аль ч шингэний хувьд зунгааралт нь температур болон найрлагаасаа хамаардаг. Хий эсвэл бусад шахагдах шингэний хувьд температураас хамаарах ба заримдаа даралтаас хамаарах тал бий.

Зарим шингэний зунгааралт нь бусад хүчин зүйлээс хамаарч болно. Тухайлбал соронзон реологийн шингэнүүд соронзон оронд орохдоо өтгөрч эхлэх ба хатуу материалын шинж чанарыг үзүүлнэ.

Хатуу бие дахь зунгааралт

Шингэний урсгалын үед гарах зунгааралтын хүчийг хатуу биеийн шахах, сунгахад үүсэх харимхайн хүчтэй адилтгаж болохгүй. Хүчдэл нь хатуу биеийн хувьд сунах хэв гажилттай хамааралтай бол, шингэнд хугацааны туршид шилжилиийн утгатай хамаатай байна. (Иймийн учир, Максвелл шингэнд түр зуурын налархай чанар байдаг гэж үзжээ.)

Гэхдээ ихэнх шингэн гэнэтийн хүчдэлд харимхай хатуу материал шиг шинж чанарыг үзүүлнэ. Эсрэгээрээ, ихэнх "хатуу бие" (боржин хүртэл) маш жижиг хүчдэлд ч гэсэн маш аажмаар шингэн шиг урсах боломжтой. Эдгээр материал нь тухайн нөхцөлд харимхайн (деформацийн үйлчлэл) болон зунгааралтын (деформацийн утгын үйлчлэл) шинж чанарыг хамтад нь агуулах учир зунгаарсан чанар гэж нэрлэгдэнэ.

Үнэхээрийн зарим судлаачид шил, полимер гэх мэт материалыг шингэн шиг маш өндөр зунгааралттай байх учир аморф хатуу материал гэж нэрлэдэг (ж.н 10¹² Па·с- ээс их). . Гэтэл бусад судлаачид энэ таамаглалыг няцааж ердийн хатуу материал урсахгүй байх хүчдэлийн хязгаарыг авч үзэх шаардлагатай гэж үздэг ба энэ нь шилний хувьд эргэлзээтэй байдаг.

Зунгаарсан хатуу нь хүчдэлийн зунгааралт болон бөөмийн зунгааралтыг хамтад нь харуулна. Сунасан зунгааралт нь уртсаж сунасан уян материалын хариу үйлдлийг илэрхийлэх шүргэх болон эзлэхүүний зунгааралтуудын шугаман хослол юм. Энэ хэмжигдэхүүн нь полимерийн шинж чанарт маш чухал ойлголт юм.

Геологид, зарим хөрс тэдгээрийн налархай шилжилтээс 3 дахин их байх зунгааралтын чанарыг харуулдаг ба тэднийг заримдаа Реид гэж нэрлэнэ.

Зунгааралтыг хэмжих

Зунгааралтыг өөр өөр төрлийн зунгааралт хэмжигч болон реометр - ээр хэмжинэ. Реометр нь зунгааралт хэмжигчээр хэмжих боломгүй, олон хүчин зүйлээс хамаарах зунгааралттай шингэнд хэрэглэгдэнэ. Шингэний температурыг тохиуулж хянах нь маш нарийн зунгааралтыг хэмжих үндэс болдог. Ялангуяа тосолгооний шингэнүүд 5 °C-ийн өөрчлөлтөнд 2 дахин их зунгааралтын утга харуулах жишээтэй.

Зарим шингэний хувьд зунгааралт нь шүргэх утгын өргөн хүрээнд тогтмол байж болно (Ньютоны шингэнүүд). Тогтмол зунгааралтгүй шингэнүүдийн (Ньютоны бус шингэн) зунгааралтын нэг тоогоор тодорхойлох боломжгүй. Ньютоны бус шингэнүүд нь шүргэх хүчдэл, шүргэх утгаас хамаарсан маш олон зунгааралтын утгуудийг өгнө.

Шингэний кинематик зунгааралтыг хэмжих хамгийн энгийн багаж нь зунгааралтыг хэмжих капиляр шил юм.

Бүрхүүл хальс хийдэг үйлдвэрт зунгааралтыг тусгай аягаар хэмждэг. Тэдгээрт Зан аяга, Фордын аяга- зэрэг хэрэглэгдэх ба үйлдвэр бүрт өөр байна. Цүлхэлтийн хугацаагаар /аягаар/ хэмжсэн зунгааралтын утгыг хөрвүүлэх тэгшитгэл ашиглан кинематик зунгааралтруу шилжүүлж болно (сантистокес, cСт).

Зарим үйлдвэрт Стормерийн зунгааралт хэмжигчээр зунгааралтыг хэмжих ба энэ нь зунгааралтыг Кребийн нэгжээр (KU) тодорхойлно.

Чичиргээнт зунгааралт хэмжигч гэж байна. Сунасан зунгааралтыг реометрээр хэмжинэ. Бөөмийн буюу эзлэхүүний зунгааралтыг акустик реометрээр хэмжинэ.

Нэгж

Динамик зунгааралт μ

Динамик зунгааралтын Си нэгж нь паскаль-секунд (Па·с), (энэ нь (Н·с)/м², эсвэл кг/(м·с)) юм. Хэрэв 1 Па·с зунгааралттай шингэн хоёр зэрэгцээ хавтгайн гол байна гэж үзвэл нэг хавтгай нь 1 паскалийн шүргэх хүчдэлээр хажуу тийш түлхэгдэж нэг секундэд хоёр хавтгайн хоорондын зайтай тэнцүү зайг туулна гэсэн үг. 20 °C тай ус нь 0.001002 Па·с-ийн зунгааралттай байх бол ердийн моторын тосны зунгааралт 0.250 Па·с гэсэн хэмжээстэй байна

Динамик зунгааралтын СГС физикийн нэгж нь поис (П) юм. Үүнийг Жеан Леонард Марие Поузиеллийн нэрийг мөнхөлж нэрлэсэн байна. Энэ нь Америкийн стандартад түгээмэл хэрэглэгдэх ба Сэнтипоис (cП) гэж тэмдэглэгдэнэ. 20 °C -тай ус нь 1.0020 cП гэсэн зунгааралттай байна.

1 П = 0.1 Па·с,

1 cП = 1 мПa·с = 0.001 Пa·с = 0.001 Н·с·м^-2 = 0.001 кг·м^-1·с^-1.

Кинематик зунгааралт ν

Кинематик зунгааралтын Си нэгж нь м²/с юм.

СГС физик нэгжид кинематик зунгааралтын нэгж нь Стокесоор (Ст) тэмдэглэгдэнэ. Мөн л Георге Габриел Стокесийн дурсгалд зориулж ийнхүү нэрэлжээ. Үүнийг заримдаа сентиСтокесоор тэмдэглэнэ (cСт). АНУ-д Стокесийг дангаар нь хэрэглэнэ.

1 Ст = 1 cм²·с⁻¹ = 10⁻⁴ м²·с⁻¹.

1 cСт = 1 мм²·с⁻¹ = 10⁻⁶ м²·с⁻¹.

20 °C -тай ус нь 1 cСт гэсэн зунгааралттай байна.

Кинематик зунгааралтыг заримдаа моментын тархалт гэж нэрлэж ашиглах тал бий. Учир нь энэ нь дулаан тархалт, масс тархалт мэттэй адил төстэй физик хэмжигэдхүүн болно.

Шингэрэлт буюу өтгөрөлт

Зунгааралтын урвуу хэмжигдэхүүн нь шингэрэлт бөгөөд түүнийг ихэвчлэн φ = 1 / μ эсвэл F = 1 / μ гэж тэмдэглэнэ. Хэмжих нэгж нь урвуу поис (cм·с·гр⁻¹) эсвэл ре гэнэ. Инженерийн практикт ховор хэрэглэгдэнэ.

Шингэрэлтийн ухагдахуун нь идеал шийдлийн зунгааралтыг тодорхойлоход хэрэглэгддэг. Хоёр өөр $a$ ба $b$ гэсэн бүрэлдэхүүнүүд холилдох үед тэдгээрийн шингэрэлт нь

$F\approx \chi _{a}F_{a}+\chi _{b}F_{b},$,

болох ба зунгааралтын эквивалент тэгшитгэл нь:

$\mu \approx {\frac {1}{\chi _{a}/\mu _{a}+\chi _{b}/\mu _{b}}},$

болно. Энд χ_a ба χ_b нь тус хольц бүрийн молийн фракцууд, μ_a болон μ_b нь тус бүрийн цэвэр зунгааралтууд болно.

Стандарт бус нэгж

Реун нь Британичуудын хэрэглэдэг динамик зунгааралтын нэгж юм.

Зунгааралтын индекс нь температураас хамааралтай кинематик зунгааралтын өөрчлөлтийг хэмжихэд хэрэглэгддэг. Энэ нь авто машины үйлдвэрлэлд тосолгооний шинж чанарыг тодорхойлоход хэрэглэгдэнэ.

Газрын тосны зарим компаниуд зунгааралтыг Саиболт хэмээх багажаар хэмжих Саиболт универсал секунд гэсэн (СУС) нэгжээр тэмдэглэдэг байна. Харин СУС-ийг сентиСкотруу ASTM D 2161 гэсэн стандартад өгөгдсөн хүснэгтийн дагуу шилжүүлнэ.

Молекул гаргалгаа

Давирхай нь уснаас ойролцоогоор 230 тэрбум (2.3X10¹¹) дахин их зунгааралттай.

Системийн зунгааралт нь сиситем дахь хоёр молекулын харилцан үйлчлэлээр тодорхойлогдох боловч одоогоор яг таг тайлбарлах энгийн илэрхийлэл алга байна. Хамгийн энгийн гэж хэлж болох илэрхийлэл нь 1985 Эван болон Моррис нарын гаргасан Хугацааны шилжилтийг засварлах функц эсвэл шугаман шүргэх зунгааралтын хувьд Греен-Кобу хамаарал зэрэг болно. Гэсэн ч дээрх хоёр илэрхийлэл нь Молекул динамикийн компьютер тооцоололд зунгааралтыг тооцоход нарийн үр дүнгүүдийг өгнө.

Хийнүүд

Хийн зунгааралт нь цэвэр молекулуудын тархалтаас гаралтай. Хийн кинетик онол нь шингэний зунгааралтын шинж чанарыг ойролцоолоход тус болдог.

Онол хүчинтэй байгаа хүрээнд:

• Зунгааралт нь даралтаас хамааралгүй ба
• зунгааралт нь температурын өсөлттэй хамт өснө.

Ж.Максвелл 1866 онд хийн зунгааралтын талаар алдартай өгүүллээ хэвлүүлсэн байдаг. Яагаад зунгааралт нь даралтаас үл хамааралтай вэ гэдгийг ойлгохын тулд А ба В гэсэн зэрэгцээ хоёр хязгаарын үеийг авч үзэх хэрэгтэй. Хийн дотоод үрэлт нь (зунгааралт) момент тархалтаас үүдэлтэй В үерүү нэвтрэн орж байгаа А үеийн бөөмийн магадлалаар тодорхойлогдоно. Максвеллийн тооцоолол нь зунгааралтын коэффициент нь нягттай, дундаж чөлөөт мөртэй, атомын дундаж хурдтай пропорциональ гэдгийг харуулдаг. Өөрөөр хэлбэл, чөлөөт дундаж мөр нь нягттай урвуу хамааралтай. Даралтын нэмэгдлээр бий болох нягтын нэмэгдэл нь зунгааралтыг өөрчилж чадахгүй.

Тархах эгэл хэсгийн дундаж чөлөөт мөртэй холбогдох нь

Тархалттай холбогдоход кинематик зунгааралт нь шингэрсэн материалын массын тархалтыг ойлгоход чухал үүрэг гүйцэтгэнэ. Зунгааралт нь шүргэх хүчдэлтэй мөн шингэний шүргэх утгатай хамааралтай ба шүргэх утга нь бөөмийн тархалт, дундаж чөлөөт мөртэй λ хамааралтай байна.

Шингэний механикаасfНьютоны шингэний хувьд өөртэйгээ зэрэгцээ хөдөлж байгаа хавтгайн нэгж талбай дээрх шүргэх хүчдэл τ нь ут талбайд пердендукляр байх зай хурдны өөрчлөлтийн харьцаагаар

$\tau =\mu {\frac {\mathrm {d} u_{x}}{\mathrm {d} y}}$

гэж тодорхойлогдно. Хэвтээ тэнхлэгийн хувьд Х-Z хавтай дээр. Бид μ -г хэрхэн λ-тай холбогдохыг харуулж дээрх тэгшитгэлийг гаргана.

Шүргэх хүчдэлийг нэгж хугацаан дахь моментын өөрчлөлтөөр илэрхийлбэл p нэгж A (моментын цүлхэлтийн утга) талбайд дурын гадаргууд

$\tau ={\frac {\dot {p}}{A}}={\frac {{\dot {m}}\langle u_{x}\rangle }{A}}.$

байх ба $\langle u_{x}\rangle$ нь х тэнхлэгийн дагуух дундаж хурд болно.

Цаашдын боловсруулалт нь

${\dot {m}}=\rho {\bar {u}}A$ болно.

$\langle u_{x}\rangle ={\frac {1}{2}}\,\lambda {\frac {\mathrm {d} u_{x}}{\mathrm {d} y}}$ молекулуул 0 ба λ (тэнцүү түгээгдсэн молекул) гэсэн зайнд тэнэх ба тэдгээрийн дундаж хурд нь зайтай шугаман өөрчлөлттэй байна гэдгийг өмнөхөөр илэрхийлж болно (λ-ийн бага утгад ямагт үнэн). Эндээс:

$\tau =\underbrace {{\frac {1}{2}}\,\rho {\bar {u}}\lambda } _{\mu }\cdot {\frac {\mathrm {d} u_{x}}{\mathrm {d} y}}\;\;\Rightarrow \;\;\nu ={\frac {\mu }{\rho }}={\tfrac {1}{2}}\,{\bar {u}}\lambda ,$

гэж гарах ба

${\dot {m}}$ нь гадаргыг цохих шингэний массын утга,

ρ шингэний нягт,

ū молекулын дундаж хурд (${\bar {u}}={\sqrt {\langle u^{2}\rangle }}$),

μ динамик зунгааралт зэрэг болно.

Хийн зунгааралтанд температурын нөлөөлөл

Сутерландын томьёо нь идеаль хийн динамик зунгааралтыг температураас хамааралтай байхаар илэрхийлнэ:

${\mu }={\mu }_{0}{\frac {T_{0}+C}{T+C}}\left({\frac {T}{T_{0}}}\right)^{3/2}.$

Энэ нь

$\lambda \,{\frac {T^{3/2}}{T+C}}\,,$-тэй тэнцүү байх ба  $\lambda ={\frac {\mu _{0}(T_{0}+C)}{T_{0}^{3/2}}}\,$  нь хийн хувьд тогтмол байна.

Сутерландийн томьёонд

• μ = Т өгөгдсөн температур дахь динамик зунгааралт (Па·с эсвэл μПa·с),
• μ₀ = жишиг температур дахь жишиг зунгааралт
• T = өгөгдсөн температур (келвин),
• T₀ =жишиг температур (келвин),
• C = Авч үзэж байгаа шингэний/хийн Сутерландын тогтмол.

Энэ томьёо нь температурын 0 < T < 555 K хүрээнд, даралтын алдаа 10% , даралтын утга 3.45 MPa -аас бага байхад хүчинтэй.

Зарим хийн хувьд Сутерландийн тогтмол болон λ -ийн утгуудийг дараах хүснэгтээс авч болно.

Gas	C [K]	T0 [K]	μ0 [μPa s]	λ [μPa s K-1/2]
air	120	291.15	18.27	1.512041288
nitrogen	111	300.55	17.81	1.406732195
oxygen	127	292.25	20.18	1.693411300
carbon dioxide	240	293.15	14.8	1.572085931
carbon monoxide	118	288.15	17.2	1.428193225
hydrogen	72	293.85	8.76	0.636236562
ammonia	370	293.15	9.82	1.297443379
sulfur dioxide	416	293.65	12.54	1.768466086
helium	79.4	273	19	1.484381490

Шингэрүүлсэн хийн зунгааралт

Чапман-Энскогийн тэгшитгэл нь шингэрүүлсэн хийн хувьд зунгааралтыг тооцоход хэрэглэгдэж болох юм. Энэ тэгшитгэл нь хагас онолын нөхцлийг ашигласан байдаг. Тэгшитгэл нь гурван ширхэг туршилтын параметрийг шаардана. Мөргөлдөөний параметр (σ), Больцманы тогтмолд хуваагдсан татах хамгийн их энерги (є/к) ба мөргөлдөөний интеграл (ω(T^*)) зэрэг юм.

${\mu }_{0}\times 10^{6}={2.6693}{\frac {(MT)^{1/2}}{\sigma ^{2}\omega (T^{*})}},$

энд

• T^* = κT/ε — багасгасан температур (хэмжээсгүй),
• μ₀ = шингэрүүлсэн хийн зунгааралт (μПa.с),
• M = моллийн масс (гр/моль),
• T = Температур (K),
• σ =мөргөлдөөний диаметр (Å),
• ε / κ = Больцманы тогтмолд хуваагдсан татах хамгийн их энерги (K),
• ω_μ = мөргөлдөөний интеграл зэрэг байна.

Дуслын шингэнүүд

Энэ бичлэг нь өөр өөр зунгааралттай шингэнүүдийг харуулна.

Шингэн буу дусал үүсгэх боломжтой шингэнд молекул хоорондын нэмэлт хүч маш чухал болж ирнэ. Энэ нь цаашид шүргэх хүчдэлийн утгад нөлөөлөх ба их маргаантай асуудал юм. Тэгэхээр шингэний хувьд:

• Зунгааралт нь даралтаас үл хамаарах (маш өндөр даралтанд өөр болно); ба
• Зунгааралт нь температур өсөхөд буурах хандлагатай (тухайлбал, усны зунгааралт нь 0 °C аас 100 °C-ын температурт тус бүр 1.79 cП ба 0.28 cП гэсэн утгатай байна).

Шингэний динамик зунгааралт нь хийн динамик зунгааралтаас хэдэн эрэмбээр их утгатай байна.

Холигдсон шингэний зунгааралт

Хоёр ба түүнээс олон шингэний хольцын зунгааралтыг Рефутасын тэгшитгэл ашиглан олно. Тооцоолол нь дараах гурван алхамд гүйцэтгэгдэнэ.

Эхний алхам нь хольцийн бүрдүүлэгч бүрт зунгааралтын холигдолтын тоог (VBN) (мөн холигдолтын индекс гэж нэрлэж болно)

(1) ${\mbox{VBN}}=14.534\times \ln \left[\ln(\nu +0.8)\right]+10.975\,$

гэж тодорхойлох ба энд кинематик зунгааралт нь сентиСтокесийн нэгжээр (cСт) байна. Бүх зунгааралтууд ижил температурт хэмжигдсэн эсхүл тооцогдсон байх ёстой.

Дараагийн алхам нь хольцын хувьд VBN -ийг

(2) ${\mbox{VBN}}_{\text{Blend}}=\left[x_{A}\times {\mbox{VBN}}_{A}\right]+\left[x_{B}\times {\mbox{VBN}}_{B}\right]+\cdots +\left[x_{N}\times {\mbox{VBN}}_{N}\right]\,$

гэж тогтоох явдал ба x_X нь хольцын хувьд бүрдүүлэгчүүдийн массын фракц юм.

Нэгэнт хольцын зунгааралтын холигдолтын тоо олдсон бол сүүлчийн алхам нь тэгшигэл (1) ээс ν тодорхойлох ажил болно.

(3) $\nu =\exp \left(\exp \left({\frac {{\text{VBN}}_{\text{Blend}}-10.975}{14.534}}\right)\right)-0.8,$

энд VBN_Blend хольцын зунгааралтын холигдолтын тоо болно.

Түгээмэл бодисын зунгааралт

Агаар

Температур 300, 400 ба 500 K үе дахь хуурай агаарын динамик зунгааралтын даралтаас хамаарах хамаарал

Агаарын зунгааралт нь температураас хамаарна. 15 °C-тай үед агаарын зунгааралт 1.81X10⁻⁵ кг/(м·с), 18.1 μПаa.с эсвэл 1.81X10⁻⁵ Пa.с байна. Харин 15 °C үед кинематик зунгааралт нь 1.48X10^-5 м²/с эсвэл 14.8 cСт байна. 25 °C үед зунгааралт нь 18.6 μПa.с ба кинематик зунгааралт 15.7 cСт байна. Тепмератураас хамаарсан зунгааралтын функцаас зунгааралтыг мөн олж болно Хийн зунгааралт тооцогч.

Ус

Усны динамик зунгааралт

Усны динамик зунгааралт нь 25 °C хэмтэй үед 8.90 × 10⁻⁴ Па·с эсвэл 8.90 × 10⁻³ дин·с/cм².
Ус нь 25 °C-т 0.0091 поис зунгааралттай ба 20 °C-т 1 сэнтиПоис зунгааралттай байна.
Температурын функцаар илэрхийлбэл T (K): (Пa·с) = A × 10^B/(T−C)
ба энд A=2.414 × 10⁻⁵ Пa·с ; B = 247.8 K ; ба C = 140 K байна.

Буцлах цэг хүртэлх өөр өөр температуртай үеийн усны зунгааралтыг доорхи хүснэгтэнд өгөв.

Temperature [°C]	Viscosity [mPa·s]
10	1.308
20	1.002
30	0.7978
40	0.6531
50	0.5471
60	0.4658
70	0.4044
80	0.3550
90	0.3150
100	0.2822

Бусад бодисууд

Ус ба сүүний зунгааралтын жишээ. Өнгдөр зунгааралттай шингэн нт адил хурдтай цутгахад бага хэмжээний цацалт үүсгэнэ.

Зөгийн бал гоожиж байна.

Самрын нухаш бол хагас хатуу шингэн бөгөөд налархай чанараа сайн хадгалдаг.

Бусад Ньютоны шингэний зунгааралтуудыг дараах хүснэгтээр өгөв:

100 kПa даралттай үед зунгааралт [μПa·с]

Gas	at 0 °C (273 K)	at 27 °C (300 K)
air	17.4	18.6
hydrogen	8.4	9.0
helium		20.0
argon		22.9
xenon	21.2	23.2
carbon dioxide		15.0
methane		11.2
ethane		9.5

Янз бүрийн хольц, нэгдмэл шингэний хувьд зунгааралт

Fluid	Viscosity [Pa·s]	Viscosity [cP]
blood (37 °C)	(3–4)X10-3	3–4
honey	2–10	2,000–10,000
molasses	5–10	5,000–10,000
molten glass	10–1,000	10,000–1,000,000
chocolate syrup	10–25	10,000–25,000
molten chocolate*	45–130	45,000–130,000
ketchup*	50–100	50,000–100,000
lard	&0000000000000100.000000100	&.100,000
peanut butter*	&0000000000000250.000000250	&0000000000250000.000000250,000
shortening*	&0000000000000250.000000250	&0000000000250000.000000250,000

Шингэний зунгааралт
(25 °C -тай үед)

Liquid :	Viscosity [Pa·s]	Viscosity [cP=mPa·s]
acetone	&-1-1-10000000000000.0003060	&0000000000000000.3060000.306
benzene	&-1-1-10000000000000.0006040.001	&0000000000000000.6040000.604
castor oil	&0000000000000000.9850000.985	&0000000000000985.000000985
corn syrup	&0000000000000001.3806001.3806	&0000000000001380.6000001,380.6
ethanol	&-1-100000000000000.0010740.001	&0000000000000001.0740001.074
ethylene glycol	&-1000000000000000.0161000.016	&0000000000000016.10000016.1
glycerol (at 20 °C)	&0000000000000001.2000001.2	&0000000000001200.0000001,200
HFO-380	&0000000000000002.0220002.022	&0000000000002022.0000002,022
mercury	&-1-100000000000000.0015260.002	&0000000000000001.5260001.526
methanol	&-1-1-10000000000000.0005440.001	&0000000000000000.5440000.544
motor oil SAE 10 (20 °C)	&-1000000000000000.0650000.065	&0000000000000065.00000065
motor oil SAE 40 (20 °C)	&0000000000000000.3190000.319	&0000000000000319.000000319
nitrobenzene	&-1-100000000000000.0018630.002	&0000000000000001.8630001.863
liquid nitrogen @ 77K	&-1-1-10000000000000.0001580	&0000000000000000.1580000.158
propanal	&-1-100000000000000.0019450.002	&0000000000000001.9450001.945
olive oil	&-1000000000000000.0810000.081	&0000000000000081.00000081
pitch	&0000000230000000.0000-0230,000,000	&0000230000000000.000000230,000,000,000
sulfuric acid	&-1000000000000000.0242000.024	&0000000000000024.20000024.2
water	&-1-100000000000000.0008940.001	&0000000000000000.8940000.894

Хатуу материалын зунгааралт

Solid	Viscosity [Pa·s]	Temperature [K]
asthenosphere	&000000000000000-4.00000070,000,000,000,000,000,000	900 °C
upper mantle	(0.7-1.0)X1021	1300-3000 °C
lower mantle	(1.0-2.0)X1021	3000-4000 °C

* эдгээр шингэнүүд нь маш өндөр зунгааралттай Ньютоны бус шингэнүүд юм.

тэмдэглэл: Өндөр зунгааралттай гэдэг нь өтгөн шинж чанартайг харуулна.

Зуурмагийн зунгааралт /булинга/

Эйнштэйн Симха, Томас, ба Китано нарын тэгшитгэлээс тодорхойлсон харьцангуй зунгааралт μ_r -ын графикууд

Булинга хэмээх нэршил нь шингэн ба хатуу бодисуудын холимогыг илэрхийлэх ба заримдаа шингэрэлтийг илэрхийлнэ. Булингын зунгааралт нь шингэн фазын зунгааралттай харьцангуйгаар талбарлагдана:

$\mu _{s}=\mu _{r}\cdot \mu _{l},$

энд μ_s ба μ_l булинга ба шингэний динамик зунгааралтууд (Пa·с), ба μ_r харьцангуй зунгааралт (хэмжээсгүй) болно.

Хатуу хэсгийн концентариц болон фракцаас хамаарч хатуу хэсгийн эзлэхүүний фракцаас ɸ хамаарсан хэд хэдэн харьцангуй зунгааралтыг илэрхийлэх загварууд байна.

Нарийн ширхэглэлтэй хатуу хэсэг хэт бага концентарицтай байвал Эйнштэйний тэгшитгэл хэрэглэгдэж болох:

$\mu _{r}=1+2.5\cdot \phi$

Харин өндөр концентарицтай үед Гут болон Симха нарын дэвшүүлсэн засвартай тэгшитгэл ашиглагдах ба энэ нь хатуу хэсгүүдийн хоорондох харилцан үйлчлэлийг авч үзнэ:

$\mu _{r}=1+2.5\cdot \phi +14.1\cdot \phi ^{2}$

Цаашилбал энэ тэгшитгэл нь Томас -аар засварлагдаж туршилтын өгөгдөлтэй тохируулагдан

$\mu _{r}=1+2.5\cdot \phi +10.05\cdot \phi ^{2}+A\cdot e^{B\cdot \phi },$

болох ба энд A = 0.00273 ба B = 16.6 байна.

Өндөр шүргэх хүчдэлүүдтэй үед (1 kПa-аас дээш), Китано нарын боловсруулсан тэгшитгэл хайлмал полимерын

$\mu _{r}=\left(1-{\frac {\phi }{A}}\right)^{-2},$

гэж итэгшитгэл ашиглагдах ба гөлгөр ширхэглэлтэй үед А = 0.68 байна.

Аморф материалын зунгааралт

Ердийн шилний зунгааралтын муруй.

Аморф материал дахь шингэний зунгааралт (тухайлбал шилнүүд ба хайлшууд) дулааны процессоор идэвхиждэг:

$\mu =A\cdot e^{Q/RT},$

энд Q идэвхижүүлэх дулааны энерги, T нь температур, R нь хийн молийн тогтмол ба A нь ойролцоолсон тогтмол юм.

Аморф материал дахь зунгааралдсан урсгал нь Аррениусын төрлийн шинж чанараас гажсан характеристиктай байна: Q нь бага температур (шилэн төлөв) дахь өндөр Q_H утгаас их температурт (шингэн төлөв) бага Q_L утга хүртэлх өөрчлөлт. Энэ өөрчлөлтөөс хамаарч, аморф материал нь дараах байдлаар ангилагдана.

• хүчтэй: Q_H − Q_L < Q_L эсвэл
• хэврэг: Q_H − Q_L ≥ Q_L.

Аморф материалын хэврэгшилт нь Доремусын хэврэгшилтийн харьцаагаар тооцогдох:

$R_{D}={\frac {Q_{H}}{Q_{L}}}$

ба хүчтэй, хатуу материалд R_D < 2 байх бол хэврэг материалд R_D ≥ 2 байна.

B₂O₃ хувьд температур ба зунгааралтын лог муруй хоёр горимыг харуулж байна.

Аморф материалын зунгааралт нв хоёр експоненттой функцаар яг таг тодорхойлогдоно:

$\mu =A_{1}\cdot T\cdot \left[1+A_{2}\cdot e^{B/RT}]\cdot [1+C\cdot e^{D/RT}\right],$

Энд A₁, A₂, B, C ба D нь аморф материалын барьцалдалтын термодинамик шинж чанартай холбооттой байна.

Шилний шилжилтийн температураас холгүй T_g дээрх тэгшитгэл нь Вогел-Фулчер-Тамманн (VFT) тэгшитгэлээр ойролцоологдоно.

Хэрэв температур нь шилний шилжилтийн температураас нилээд бага бол T ≪ T_g хоёр экспонент тэгшитгэл нь Арренуисын төрлийн тэгшитгэлээр,

$\mu =A_{L}T\cdot e^{Q_{H}/RT}$

гэж илэрхийлэгдэх ба энд

$Q_{H}=H_{d}+H_{m},\,$

мөн H_d нь эвдэрсэн барьцалдалтын бүрэлдэлтийн энтальпи (тэмдэглэхдээ configuron s) ба H_m нь тэдгээрийн хөдөлгөөний энтальпи болно. Хэрэв температур нь шилний шилжилтийн температураас бага бол, T < T_g, зунгааралтын идэвхижүүлэх энерги нь өндөр байна. Яагаад гэвэл аморф материалууд шилэн төлөвт байхдаа тэдгээрийн барьцалдалт нь эвдрээгүй байдаг.

Хэрэв температур нь шилний шилжилтийн температураас өндөр бол T ≫ T_g хоёр экспонент тэгшитгэл нь Аррениусын төрлийн тэгшитгэлээр:

$\mu =A_{H}T\cdot e^{Q_{L}/RT},$

байх ба энд

$Q_{L}=H_{m}.\,$

мөн температур нь шилний шилжилтийн температураас их бол T > T_g аморфи материалууд нь хайлмал тэдгээрийн барьцалдалт нь эвдэрсэн, хөнгхөн урсамтгай болсон байх учир зунгааралтын идэвхижүүлэх энерги нь бага байна.

Хуйлралтын зунгааралт

Шингэний урсгалын турбулент судалгаанд ерөнхийдөө бага хэмжээтэй хуйлралтууд (эсвэл хуй угалзууд) -ийг ялгасаж үзэх ба том хэмжээст хуйлралтуудыг тооцож хуйлралтын зунгааралт хэмээхийг авч үзнэ. Энэ нь бага хэмжээстэй урсгалд энергийн сарнилт болон зөөгдөлтийг тодорхойлдог (том хуйлралтын симуляци гэдгийг үзэх). Далайн циркуляцийн загварчлалд хэрэглэгдэх хуйлралтын зунгааралтын утгыг 5×10⁴ -аас 10⁶ Пa·с хооронд тооцооны торны нарийвчлалаас хамааруулж авна.

Мөн үзэх

• Deborah number
• Dilatant
• Herschel–Bulkley fluid
• Hyperviscosity syndrome
• Intrinsic viscosity
• Inviscid flow
• Morton number
• Relative viscosity
• Reyn
• Reynolds number
• Trouton's ratio
• Two-dimensional point vortex gas
• Viscoelasticity
• Viscosity index
• Joback method (estimation of the liquid viscosity from molecular structure)
• Microviscosity
• Rheology
• Superfluid helium-4
• Stokes flow

Цааш унших

• Hatschek, Emil (1928). The Viscosity of Liquids. New York: Van Nostrand. Загвар:Oclc.
• Massey, B. S.; Ward-Smith, A. J. (2011). Mechanics of Fluids (Ninth ed.). London; New York: Spon Press. ISBN 978-0-415-60259-4. OCLC 690084654.

Гадаад линк

Wiktionary

Wiktionary: Зунгааралт – Энэ үгийг тайлбар толиос харна уу

• Fluid properties High accuracy calculation of viscosity and other physical properties of frequent used pure liquids and gases.
• Gas viscosity calculator as function of temperature
• Air viscosity calculator as function of temperature and pressure
• Fluid Characteristics Chart A table of viscosities and vapor pressures for various fluids
• Gas Dynamics Toolbox Calculate coefficient of viscosity for mixtures of gases
• Glass Viscosity Measurement Viscosity measurement, viscosity units and fixpoints, glass viscosity calculation
• Kinematic Viscosity conversion between kinematic and dynamic viscosity.
• Physical Characteristics of Water A table of water viscosity as a function of temperature
• Vogel–Tammann–Fulcher Equation Parameters
• Calculation of temperature-dependent dynamic viscosities for some common components
• "Test Procedures for Testing Highway and Nonroad Engines and Omnibus Technical Amendments". United States Environmental Protection Agency
• Artificial viscosity